7329. Строительство

После завершения строительства дачного домика у Степана осталось n деревянных досок длиной l₁, ..., l_n. Он решил использовать их для постройки мостика, с которого будет удобно ловить рыбу.

Степан убеждён, что чем длиннее будет мостик, тем больше рыбы ему удастся поймать!

Кроме того, как и многие рыбаки, он суеверен и следует приметам. Согласно одной из них, мостик нужно строить только из цельных досок: доски можно разрезать, но соединять их между собой нельзя. Теперь Степан хочет узнать, какой максимальной длины d может быть мостик, если он должен состоять ровно из m досок.

Вход. Целые числа n, m, l_i (1 ≤ n ≤ 10000, 1 ≤ m, l_i ≤ 2 * 10⁹) – количество оставшихся досок, количество досок, из которых должен состоять мостик, и длины имеющихся досок.

Выход. Выведите одно целое число d – максимальную возможную длину доски для мостика, или 0, если построить мостик невозможно.

Пример входа	Пример выхода
4 6 16 12 20 10	8

РЕШЕНИЕ

бинарный поиск

Анализ алгоритма

Будем искать длину мостика d с помощью бинарного поиска. Изначально положим d Î [Left; Right] = [0; INF].

Рассмотрим следующую подзадачу: можно ли составить требуемый мостик длины в точности Mid = (Left + Right) / 2 ? Для этого посчитаем, сколько досок длины Mid можно получить из имеющихся.

Из доски длины l_i можно получить досок длины Mid. Просуммировав это значение по всем доскам, узнаем общее количество досок длины Mid, которые можно получить разрезанием:

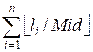
Если общее количество таких досок не менее m, то это означает, что можно попробовать увеличить длину – устанавливаем Left = Mid + 1. В противном случае уменьшаем верхнюю границу: Right = Mid.

Ответом на задачу будет значение Left – 1.

Пример

В приведённом примере имеется 4 доски. Необходимо построить мостик, состоящий из 6 досок.

Если выбрать длину доски равной 8, то из имеющихся досок можно получить

16 / 8 + 12 / 8 + 20 / 8 + 10 / 8 = 6

досок длины 8.

Если же выбрать длину 9, то получится

16 / 9 + 12 / 9 + 20 / 9 + 10 / 9 = 5,

досок, что меньше необходимого количества.

Реализация алгоритма

Определим используемые константы. Длины имеющихся досок l_i храним в массиве a.

#define INF 2000000010

#define MAX 1000009

long long a[MAX];

Функция cnt возвращает количество досок, которое можно получить из имеющихся, если каждая из них должна иметь длину в точности Mid. Это значение равно сумме

long long cnt(long long Mid)

{

if (Mid == 0) return INF;

long long res = 0;

for(i = 0; i < n; i++)

res += a[i] / Mid;

return res;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d",&n,&m);

for(i = 0; i < n; i++)

scanf("%d",&a[i]);

Установим границы для значения d Î [Left; Right] = [0; INF] и запустим бинарный поиск.

Left = 0;

Right = INF;

while (Left < Right)

{

Mid = (Left + Right) / 2;

Значение cnt(Mid) равно количеству досок, которое можно получить из имеющихся, если каждая из них должна иметь длину Mid. Если это количество меньше требуемого числа m, следует уменьшить предполагаемую длину доски: устанавливаем Right = Mid. В противном случае увеличиваем левую границу: Left = Mid + 1.

if (cnt(Mid) < m) Right = Mid;

else Left = Mid + 1;

}

Выводим ответ.

printf("%lld\n",Left - 1);