7329. Construction

After completing the construction of his country house, Stepan was left with n wooden planks of lengths l₁, ..., l_n. He decided to use them to build a small pier from which he could comfortably fish.

Stepan firmly believes that the longer the pier, the more fish he will be able to catch!

Like many fishermen, he is also superstitious and follows certain traditions. According to one of them, the pier must be built only from whole planks: planks may be cut, but they must not be joined together.

Now Stepan wants to determine the maximum possible length d of the pier if it must consist of exactly m planks.

Input. Contains integers n, m, and lᵢ (1 ≤ n ≤ 10,000; 1 ≤ m, lᵢ ≤ 2 × 10⁹) – the number of available planks, the number of planks the pier must consist of, and the lengths of the available planks.

Output. Print a single integer d – the maximum possible length of a pier plank, or 0 if building the pier is impossible.

Sample input	Sample output
4 6 16 12 20 10	8

SOLUTION

binary search

Algorithm analysis

We’ll search for the desired pier length d using binary search. Initially, let d Î [Left; Right] = [0; INF].

Let us consider the following subproblem: is it possible to build a pier consisting of exactly m planks, each of length Mid = (Left + Right) / 2 ? To check this, calculate how many planks of length Mid can be obtained from the available ones.

From a plank of length lᵢ, we can obtain planks of length Mid. By summing this value over all planks, we get the total number of planks of length Mid that can be obtained through cutting:

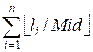
If the total number is at least m, it means we can try to increase the length – so we set Left = Mid + 1. Otherwise, reduce the upper bound: Right = Mid.

The final answer will be Left – 1.

Example

In the given example, there are 4 planks. The task is to build a pier consisting of 6 planks.

If we choose the plank length to be 8, then from the available planks we can obtain

16 / 8 + 12 / 8 + 20 / 8 + 10 / 8 = 6

planks of length 8.

If we choose the length to be 9, then we get

16 / 9 + 12 / 9 + 20 / 9 + 10 / 9 = 5

planks, which is less than the required amount.

Algorithm implementation

Let’s define the constants used. The lengths of the available planks l_i are stored in the array a.

#define INF 2000000010

#define MAX 1000009

long long a[MAX];

The function cnt returns the number of planks that can be obtained from the available ones if each plank must have an exact length of Mid. This value is equal to the sum of

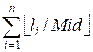
long long cnt(long long Mid)

{

if (Mid == 0) return INF;

long long res = 0;

for(i = 0; i < n; i++)

res += a[i] / Mid;

return res;

}

The main part of the program. Read the input data.

scanf("%d %d",&n,&m);

for(i = 0; i < n; i++)

scanf("%d",&a[i]);

Set the boundaries for the value of d Î [Left; Right] = [0; INF] and start a binary search.

Left = 0;

Right = INF;

while (Left < Right)

{

Mid = (Left + Right) / 2;

The value of cnt(Mid) is the number of boards that can be obtained from the available ones if each must have length Mid. If this number is less than the required m, the proposed board length should be decreased by setting Right = Mid. Otherwise, increase the lower boundary by setting Left = Mid + 1.

if (cnt(Mid) < m) Right = Mid;

else Left = Mid + 1;

}

Print the answer.

printf("%lld\n",Left - 1);