7403. Включить лампу

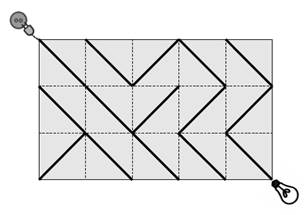
Степан разрабатывает электронную схему на прямоугольной сетке размером n × m, состоящей из квадратных плиток. Каждый из n × m квадратов имеет провод, соединяющий два противоположных угла.

Источник питания подключен к левому верхнему углу сетки, а лампа – к правому нижнему. Чтобы включить лампу, можно повернуть любую плитку на 90 градусов в любом направлении.

На изображении лампа выключена. Если повернуть любую плитку во второй колонке справа, лампа включится.

Напишите программу, которая определит минимальное количество плиток, которые нужно повернуть, чтобы включить лампу.

Вход. Первая строка содержит два целых числа n и m (1 ≤ n, m ≤ 500) – размеры сетки. Далее следуют n строк по m символов – ‘\’ или ‘/’, указывающие направление провода на каждой плитке.

Выход. Выведите минимальное количество поворотов, необходимых для включения лампы, или сообщение “NO SOLUTION”, если включить лампу невозможно.

Пример входа	Пример выхода
3 5 \\/\\ \\/// /\\\\	1

РЕШЕНИЕ

поиск в ширину

Анализ алгоритма

Пронумеруем горизонтальные и вертикальные линии прямоугольной сетки начиная с 0. Всего горизонтальных линий будет n + 1, они пронумерованы от 0 до n. Вертикальных линий будет m + 1, они пронумерованы от 0 до m. Левый верхний угол сетки имеет координаты (0, 0), правый нижний – координаты (n, m).

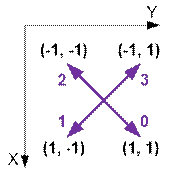
Каждому узлу сетки (i, j) поставим в соответствие вершину графа. Из каждого узла имеются 4 направления передвижения (по диагоналям). Пронумеруем направления:

Входное состояниие прямоугольной сетки и плиток на ней храним в массиве weight. Значение weight[i][j][dir] содержит вес ребра из вершины (i, j) по направлению dir (dir = 0, 1, 2, 3). Если из точки (i, j) по направлению dir идет провод, то установим weight[i][j][dir] = 0 (для передвижения плитку вращать не надо). Если точка (i, j) по направлению dir не соединена проводом, то положим weight[i][j][dir] = 1 (плитку следует повернуть). Таким образом построен взвешенный 0 – 1 граф, в котором минимальный путь между вершинами равен наименьшему числу плиток, которые следует повернуть для установления связи.

Например, для следующего примера имеют место соотношения:

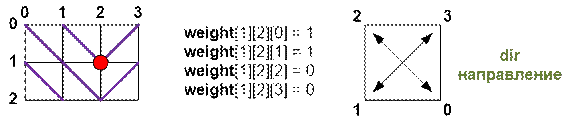
Рассмотрим процесс построения графа по входному текстовому массиву – входному состоянию сетки. Рассмотрим символ ‘/’ в клетке с левым верхом (i, j).

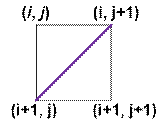
В этом случае:

· из точки (i, j) по направлению 0 двигаться нельзя и weight[i][j][0] = 1;

· из точки (i + 1, j + 1) по направлению 2 двигаться нельзя и weight[i + 1][j + 1][2] = 1;

· из точки (i, j + 1) можно двигаться по направлению 1, поэтому weight[i][j + 1][1] = 0;

· из точки (i + 1, j) можно двигаться по направлению 3, поэтому weight[i + 1][j][3] = 0;

Рассмотрим символ ‘\’ в клетке с левым верхом (i, j).

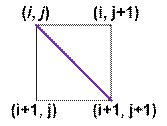
В этом случае:

· из точки (i, j) можно двигаться по направлению 0 и weight[i][j][0] = 0;

· из точки (i + 1, j + 1) можно двигаться по направлению 2 и weight[i + 1][j + 1][2] = 0;

· из точки (i, j + 1) по направлению 1 двигаться нельзя и weight[i][j + 1][1] = 1;

· из точки (i + 1, j) по направлению 3 двигаться нельзя и weight[i + 1][j][3] = 1;

Поиском в ширину ищем кратчайший путь на 0 – 1 графе из (0, 0) в (n, m).

Реализация алгоритма

Объявим константы и рабочие массивы. Входную сетку храним в массиве строк g.

#define INF 0x3F3F3F3F

#define MAX 510

int dist[MAX][MAX], weight[MAX][MAX][4];

string g[MAX];

Функция CanGo проверяет, не вышла ли точка с координатами (x, y) за границы сетки.

int CanGo(int x, int y)

{

return (x >= 0) && (x <= n) && (y >= 0) && (y <= m);

}

Функция bfs реализует поиск в ширину из точки (sx, sy).

void bfs(int sx, int sy)

{

Инициализация массивов. Пара (dx[i], dy[i]) задает направление i.

int dx[] = { 1,1,-1,-1 };

int dy[] = { 1,-1,-1,1 };

memset(dist, 0x3F, sizeof(dist));

dist[sx][sy] = 0;

deque<pair<int, int> > q;

q.push_back(make_pair(sx,sy));

Основной цикл поиск в ширину – пока очередь не пуста.

while (!q.empty())

{

Извлекаем координаты (x, y) вершины из головы очереди.

int x = q.front().first;

int y = q.front().second;

q.pop_front();

Перебираем 4 ребра – направления, куда можно попасть из (x, y). Из точки (x, y) имеется ребро в (x + dx[i], y + dy[i]) весом weight[x][y][i].

for (int i = 0; i < 4; i++)

{

int xx = x + dx[i];

int yy = y + dy[i];

if (!CanGo(xx, yy)) continue;

int w = weight[x][y][i];

Если ребро (x, y) – (xx, yy) релаксирует, то пересчитываем кратчайшее расстояние dist[xx][yy] и кладем вершину (xx, yy) или в начало или в конец очереди в зависимости от веса ребра.

if (dist[xx][yy] > dist[x][y] + w)

{

dist[xx][yy] = dist[x][y] + w;

if (w == 1)

q.push_back(make_pair(xx, yy));

else

q.push_front(make_pair(xx, yy));

}

}

}

}

Основная часть программы. Читаем входные данные.

cin >> n >> m;

for (i = 0; i < n; i++)

cin >> g[i];

Строим граф.

memset(weight, -1, sizeof(weight));

for (i = 0; i < n; i++)

for (j = 0; j < m; j++)

{

if (g[i][j] == '/')

{

weight[i][j][0] = 1;

weight[i + 1][j + 1][2] = 1;

weight[i][j + 1][1] = 0;

weight[i + 1][j][3] = 0;

}

else

{

weight[i][j][0] = 0;

weight[i + 1][j + 1][2] = 0;

weight[i][j + 1][1] = 1;

weight[i + 1][j][3] = 1;

}

}

Запускаем поиск в ширину из точки (0, 0),

bfs(0, 0);

Выводим кратчайшее расстояние до (n, m).

if (dist[n][m] == INF)

cout << "NO SOLUTION" << endl;

else

cout << dist[n][m] << endl;