7414. Простое
задание
Вам дана строка
S длины n и q запросов. Каждый запрос имеет формат i
j k, означающий что необходимо отсортировать подстроку, состоящую из символов
на позициях i до j включительно,
в неубывающем порядке, если k = 1, или
в невозрастающем порядке, если k = 0.
После выполнения
всех запросов выведите полученную итоговую строку.
Вход. В первой строке заданы два целых числа n и q (1 ≤ n ≤ 105, 0 ≤ q ≤ 50000) – длина строки и количество
запросов соответственно.
Во второй строке содержится строка S, состоящая только из
строчных латинских букв.
Каждая из следующих q
строк содержит три целых числа i, j и k
(1 ≤ i ≤ j ≤ n, k = 0 или k = 1), описывающих запрос.
Выход. Выведите строку
S после выполнения всех запросов.
|
Пример
входа |
Пример
выхода |
|
10 5 abacdabcda 7 10 0 5 8 1 1 4 0 3 6 0 7 10 1 |
cbcaaaabdd |
РЕШЕНИЕ
дерево отрезков
Анализ алгоритма
Создадим 26
деревьев отрезков для подсчёта сумм – по одному для каждой буквы от ‘a’
до ‘z’. Каждое дерево должно поддерживать множественные модификации.
Например, для
буквы ‘a’ и строки “abacdabcda” соответствующее дерево отрезков будет выглядеть так:
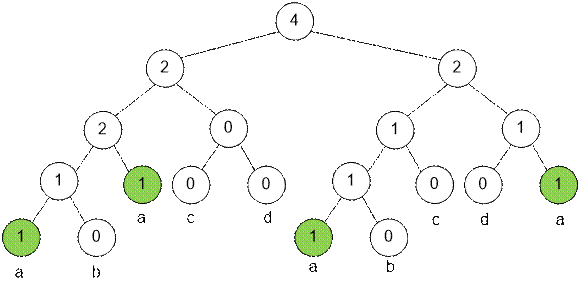
С помощью такого
дерева можно за логарифмическое время определить, сколько раз заданная буква
встречается на отрезке [l; r].
Выполнение
запроса на отрезке [l; r] сводится к сортировке подсчётом. Сначала в массиве cnt
подсчитывается, сколько раз каждая буква встречается на данном отрезке.
Далее, в
зависимости от значения k, мы “пересобираем” этот участок строки:
·
если k = 1, то символы располагаются в неубывающем порядке – то есть буквы от
‘a’ к ‘z’;
·
если k = 0, то в невозрастающем
порядке, от ‘z’ к ‘a’.
Для этого на
всём отрезке [l; r] для каждой буквы ‘a’ + j,
количество которой известно из массива cnt, мы выставляем в дереве отрезков
соответствующее количество единиц, начиная с позиции l (если сортируем по возрастанию)
или с позиции r (если по убыванию).
Например, пусть
на позициях [10; 17] находится подстрока “acbdbcab”. Подсчитаем
количество каждой
буквы на этом интервале:
·
Буква ‘a’ встречается 2 раза;
·
Буква ‘b’ встречается 3 раза;
·
Буква ‘c’ встречается 2 раза;
·
Буква ‘d’ встречается 1 раз;
Чтобы отсортировать буквы
на отрезке по возрастанию, необходимо для дерева отрезков каждой буквы сначала
обнулить значения на интервале [10; 17], а затем выполнить следующие операции:
·
Для буквы ‘a’ на отрезке [10; 11] каждому
элементу присвоить 1;
·
Для буквы ‘b’ на отрезке [12; 14] каждому
элементу присвоить 1;
·
Для буквы ‘c’ на отрезке [15; 16] каждому
элементу присвоить 1;
·
Для буквы ‘d’ на отрезке [17; 17] каждому
элементу присвоить 1;
Такое “обновление” деревьев
отрезков фактически моделирует перестановку символов на нужном участке без непосредственного
изменения самой строки.
После обработки всех
запросов итоговая строка восстанавливается из содержимого 26 деревьев отрезков:
для каждой буквы последовательно выполняется обход её дерева, и в тех позициях,
где значение равно 1, в результирующую строку записывается соответствующий
символ.
Реализация алгоритма
Для каждой буквы от ‘a’ до ‘z’ создадим собственное дерево
отрезков. Таким образом, всего используется ALPHABET = 26 деревьев, каждое из
которых поддерживает операции суммирования и множественную модификацию.
#define MAX 100010
#define ALPHABET 26
struct node
{
int sum, add;
}
SegTree[4*MAX][ALPHABET];
Объявим массив для подсчета количества вхождений каждой буквы.
int cnt[ALPHABET];
Построим 26 деревьев отрезков по строке s – по одному для каждой буквы
латинского алфавита.
void build(int v, int lpos, int rpos)
{
if (lpos == rpos)
{
SegTree[v][s[lpos] - 'a'].sum = 1;
for (int i = 0; i < ALPHABET; i++)
SegTree[v][i].add = -1;
}
else
{
int mid = (lpos + rpos) / 2;
build(v * 2, lpos, mid);
build(v * 2 + 1, mid + 1, rpos);
for (int i = 0; i < ALPHABET; i++)
{
SegTree[v][i].sum =
SegTree[v * 2][i].sum + SegTree[v * 2 + 1][i].sum;
SegTree[v][i].add = -1;
}
}
}
Вершине v соответствует
отрезок [lpos, rpos], при этом mid = (lpos + rpos) / 2. Выполним проталкивание этой вершины в дереве
отрезков с номером ver.
void Push(int v, int lpos, int mid, int rpos, int ver)
{
if (SegTree[v][ver].add != -1)
{
SegTree[2 * v][ver].add = SegTree[v][ver].add;
SegTree[2 * v][ver].sum = (mid - lpos + 1) * SegTree[v][ver].add;
SegTree[2 * v + 1][ver].add = SegTree[v][ver].add;
SegTree[2 * v + 1][ver].sum = (rpos - mid) * SegTree[v][ver].add;
SegTree[v][ver].add = -1;
}
}
Вершине v соответствует
отрезок [lpos, rpos]. В дереве отрезков с номером ver
установим значение val для всех элементов с индексами от left до right.
void SetValue(int v, int lpos, int rpos, int left, int right,
int val, int ver)
{
if (left > right) return;
if ((lpos == left) && (rpos == right))
{
SegTree[v][ver].add = val;
SegTree[v][ver].sum = (right - left + 1) * val;
return;
}
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos, ver);
SetValue(2 * v, lpos, mid, left, min(mid, right), val, ver);
SetValue(2 * v + 1, mid + 1, rpos, max(left, mid + 1), right,
val, ver);
SegTree[v][ver].sum =
SegTree[2 * v][ver].sum + SegTree[2 * v + 1][ver].sum;
}
Вершине v соответствует
отрезок [lpos, rpos]. Найдем сумму элементов на отрезке
[left; right] в дереве отрезков с номером ver.
int Summa(int v, int lpos, int rpos, int left, int right, int ver)
{
if (left > right) return 0;
if ((lpos == left) && (rpos == right)) return SegTree[v][ver].sum;
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos, ver);
return Summa(2 * v, lpos, mid, left, min(mid, right), ver) +
Summa(2 * v + 1, mid + 1, rpos, max(left, mid + 1), right, ver);
}
Выполним проталкивание во всех вершинах дерева отрезков с номером ver. Затем внесём букву ver + ‘a’ во все позиции строки s,
где ее значение
в
дереве отрезков ver равно 1.
void get(int v, int lpos, int rpos, int ver)
{
if (SegTree[v][ver].sum == 0) return;
if (lpos == rpos)
{
s[lpos] = ver + 'a';
return;
}
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos, ver);
get(2 * v, lpos, mid, ver);
get(2 * v + 1, mid + 1, rpos, ver);
}
Основная часть программы. Читаем входные данные. По входной
строке s строим 26 деревьев отрезков – по одному
для каждой буквы латинского алфавита.
cin >> n >> q;
cin >> s;
s = " " + s;
build(1,1,n);
Последовательно обрабатываем q запросов.
for (i = 0; i <
q; i++)
{
cin >> l >> r >> command;
Выполним сортировку подсчетом всех букв на отрезке [l; r]. Для этого
сначала подсчитаем количество вхождений каждой буквы ‘a’
+ j на данном интервале и запишем
результат в cnt[j].
for (j = 0; j <
ALPHABET; j++)
cnt[j] = Summa(1, 1, n, l, r, j);
Затем, начиная с позиции pos, будем двигаться вправо или влево в
зависимости от значения переменной command.
pos = (command == 1) ? l : r;
for (j = 0; j <
ALPHABET; j++)
{
if (!cnt[j]) continue;
SetValue(1, 1, n, l, r, 0, j);
if (command)
{
SetValue(1, 1, n, pos, pos + cnt[j] - 1,
1, j);
pos += cnt[j];
}
else
{
SetValue(1, 1, n, pos - cnt[j] + 1, pos,
1, j);
pos -= cnt[j];
}
}
}
Генерация результирующей строки выполняется на основе содержимого деревьев
отрезков. Функция get(1, 1, n, i), используя
данные i-го дерева отрезков, расставляет все буквы ‘a’ + i на соответствующие позиции строки s. Функция get выполняет
полное проталкивание данных, проходя по всем вершинам дерева отрезков за время
O(n).
for (i = 0; i <
ALPHABET; i++)
get(1, 1, n, i);
Выводим результирующую строку.
cout << s.substr(1);