7443. Graph decompositions
One day Zhomart
was solving a path routing problem related to networks. He discovered that his
underlying graph is directed and acyclic. When Serik came to see this problem
he was wonder that there are many ways to decompose Zhomart’s graph into
edge-disjoint paths. Friends now started to think in how many ways this can be
done. Please help them.
Input. First line contains two integers n and m (1 ≤ n ≤ 1000, 1 ≤ m ≤ 499500). Each of the
next m lines contains two integers i, j meaning that there is a directed
edge from vertex i to vertex j in the given graph.
Output. Print one integer
number – the answer to the problem by modulo 109 + 7.
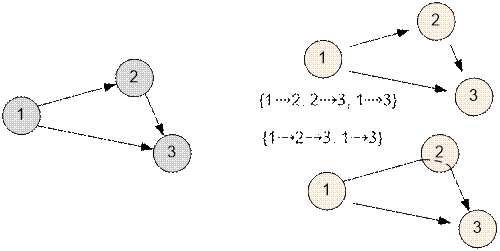
Example. There are 2 possible decompositions from
sample:
1) two paths: 1 → 2 → 3 and 1 →
3;
2) three paths: 1 → 2, 2 → 3 and
1 → 3.
|
Sample
input |
Sample
output |
|
3 3 1 2 2 3 1 3 |
2 |
SOLUTION
combinatorics
Algorithm analysis
Let’s consider in how many ways we can decompose
the edges at each vertex. The product of this number of ways for each vertex is
the answer.
Let the vertex
have x incoming and y outgoing edges. Since the graph should
be split into a set of edge-disjoint paths, we can choose i edges out of x incoming
ones, that will continue i paths, that is, they will go through
the vertex and leave it through i
outgoing edges. The rest of the incoming edges will end their paths at the
vertex, the rest outgoing ones will start their paths at the vertex.
The number of
ways to choose i edges from incoming and i edges from outgoing equals to 
. However, these i
edges can still be rearranged, that is, the specified number of ways should be
multiplied by i!
Thus, the number
of ways to decompose one vertex is
f(x, y)
= 
Let in[i] contains the number of edges incoming the vertex i, out[i] contains the number of edges outgoing from the vertex i (1 ≤ i ≤ n). Then the answer to the problem will be
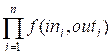
Remember that all
calculations should be done modulo 109 + 7.
Example
The directed
graph from the sample has two possible decomposition:
Consider options
for decomposition of a vertex with two input and two output edges.
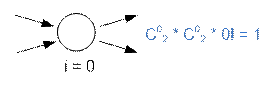
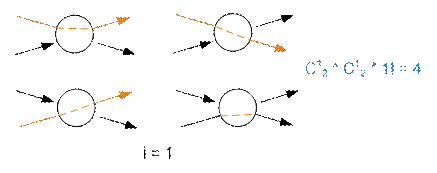
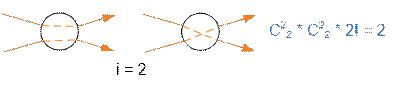
So f(2, 2) = 1 + 4 + 2 = 7.
Consider the
number of decompositions for the graph:
The answer is
= f(0, 1) * f(1, 1) * f(1, 1) *
f(1, 0) = 4
The possible
decompositions are:
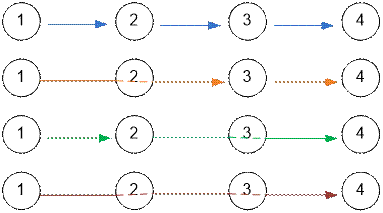
Consider the next sample.
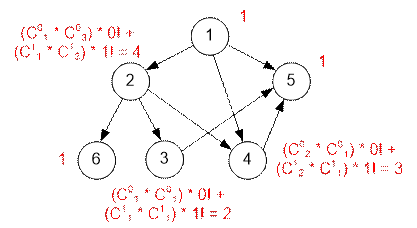
The number of
graph decompositions is 4 * 2 * 3 = 24.
Algorithm realization
Declare the arrays.
#define MOD 1000000007LL
#define MAX 1110
long long
c[MAX][MAX], in[MAX], out[MAX], fac[MAX];
Let the vertex have x
incoming and y outgoing edges. Then the number of ways to do its
decomposition equals to f(x, y).
long long
f(int x, int y)
{
long long ans = 0;
for(int i = 0; i <= min(x,y); i++)
ans = (ans + (((c[x][i] * c[y][i]) % MOD) *
fac[i]) % MOD) % MOD;
return ans;
}
The main part of the program. Fill arrays with zeroes.
scanf("%d %d",&n,&m);
memset(c,0,sizeof(c));
memset(in,0,sizeof(in));
memset(out,0,sizeof(out));
memset(fac,0,sizeof(fac));
Fill the array of binomial coefficients: c[i][j]
= 
.
c[0][0] = 1;
for(i = 0; i < MAX; i++)
c[i][0] = 1;
for(i = 1; i < MAX; i++)
for(j = 1; j
<= i; j++)
c[i][j] = (c[i-1][j] + c[i-1][j-1]) % MOD;
Fill the array of factorials.
fac[0] = 1;
for(i = 1; i < MAX; i++)
fac[i] = (fac[i-1] * i) % MOD;
Read the edges of the directed graph. Fill the arrays of incoming in and outgoing out edges.
for(i = 0; i < m; i++)
{
scanf("%d
%d",&x,&y);
out[x]++;
in[y]++;
}
Compute the product of ways in which we can make the decomposition of the edges
at each vertex.
ans = 1;
for(i = 1; i <= n; i++)
ans = (ans * f(in[i], out[i])) % MOD;
Print the answer.
printf("%lld\n",ans);