7482. Trading

Along the Almaty - Taraz highway, there are n villages, numbered from 1 to n. With the arrival of winter, m unknown traders brought knitted hats from a certain aul and began selling them in these villages.

The traders follow two principles:

· They do not sell in the same place for more than one day.

· Each day, they increase the price of a hat.

More formally, each i-th trader:

· Starts selling in village l_i with an initial price of x_i per hat.

· Moves to a neighboring village each day: if they sold in village j yesterday, they sell in village j + 1 today.

· Increases the price by 1 each day: if the price was x yesterday, today it is x + 1.

· Finishes selling in village r_i (including selling in r_i on the last day).

For each village, determine the maximum price of a single hat throughout the entire trading history.

Input. The first line contains two integers n (1 ≤ n ≤ 3 * 10⁵) and m (1 ≤ m ≤ 3 * 10⁵) – the number of villages and the number of traders, respectively.

The next m lines each contain three integers: l_i, r_i (1 ≤ l_i ≤ r_i ≤ n) and x_i (1 ≤ x_i ≤ 10⁹) – the starting and ending villages, as well as the initial price of a hat for the i-th trader.

Output. Print n integers, where the i-th number represents the maximum price of a hat throughout the entire trading history in the i-th village. If no trade took place in a particular village, print 0.

Sample inpuut	Sample output
5 2 1 3 2 2 4 6	2 6 7 8 0

SOLUTION

data structures – segment tree

Algorithm analysis

Construct a segment tree over the range [1; n] and initially set all values to zero. Suppose a trader sold hats in villages [l_i; r_i], starting with a price of p_i. Divide the segment [l_i; r_i] into fundamental segments [lx₁; ry₁], [lx₂; ry₂], …, [lx_k; ry_k]. Then, for the node corresponding to the segment [lx_q; ry_q] (1 ≤ q ≤ k), store the value

p_i + the sum of the lengths of the segments [lx_t; ry_t], for all t < q.

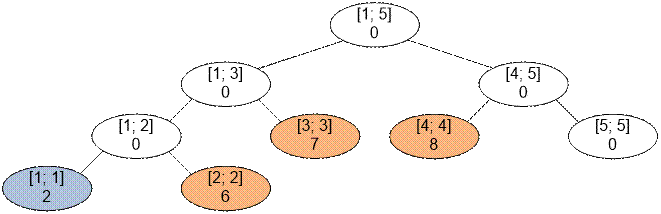
For example, let n = 5, and the first trade covers the cities numbered from 2 to 5, starting with a price of 4. Then, the segment [2; 5] will be split into fundamental segments: [2; 2], [3; 3], [4; 5]. After processing the first operation, the segment tree will look as follows:

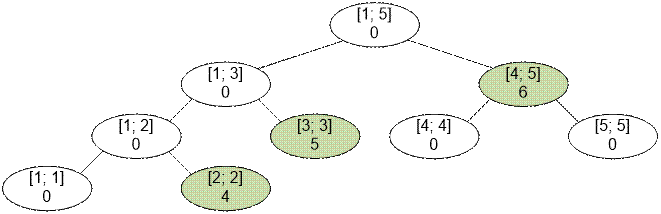
If the fundamental segment [a; b] contains the value p, it means that:

· The trader sold hats in all cities from a to b.

· In city a, the hat was sold for the price p, in city a + 1 for the price p + 1, and so on, up to city b, where the price was p + b – a.

Consider the procedure for processing the query [left; right] (the segment where the trader is trading) over the range [lpos; rpos], if the initial price of the hat is x.

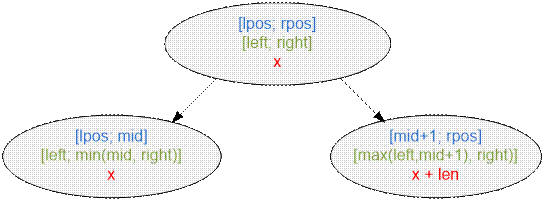
In the left subsegment, the merchant will sell hats in len = min(mid, right) – left + 1 cities, starting at the price x. In the right subsegment, the first price of the hat in the city where the merchant arrives will be x + len. Thus, in the segment with indices [max(left, mid + 1), right], the trade will start at the price x + len. However, if len < 0 (which is possible if the entire query segment lies within the right subsegment), set len = 0.

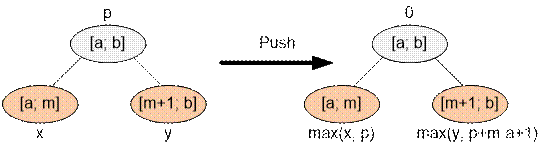
Consider the segment [a; b], which has two subsegments: [a; m] and [m + 1; b]. If the trader sold a hat for price p in city a, then in city m + 1, the price will be p + m + 1 – a.

During the query processing, implement value propagation that maintains the maximum.

To print the answer, traverse the tree, propagate all values to the leaves, and then print them.

Example

Consider the execution of the two queries given in the example. Split the query segments into fundamental segments:

· [1; 3] = [1; 3];

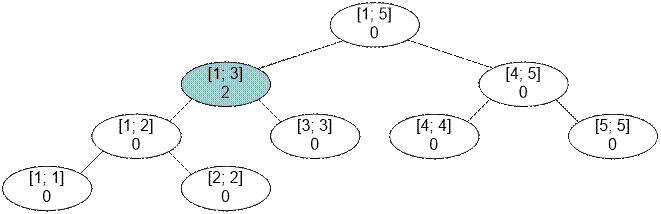
· [2; 4] = [2; 2] + [3; 3] + [4; 4].

Algorithm implementation

Declare an array SegTree to store the segment tree.

#define MAX 300010

long long SegTree[4*MAX];

The Push function propagates the value from node v to its children.

void Push(int v, int lpos, int mid, int rpos)

{

if (SegTree[v])

{

SegTree[2 * v] = max(SegTree[2 * v], SegTree[v]);

SegTree[2 * v + 1] = max(SegTree[2 * v + 1],

SegTree[v] + mid - lpos + 1);

SegTree[v] = 0;

}

}

The Update function performs the sale of hats over the segment [left; right], starting with the price x.

void Update(int v, int lpos, int rpos, int left, int right,

long long x)

{

if (left > right) return;

if ((lpos == left) && (rpos == right))

SegTree[v] = max(SegTree[v], x);

else

{

int mid = (lpos + rpos) / 2;

Push(v, lpos, mid, rpos);

int len = min(mid, right) - left + 1;

if (len < 0) len = 0;

Update(2 * v, lpos, mid, left, min(mid, right), x);

Update(2 * v + 1, mid + 1, rpos, max(left, mid + 1),

right, x + len);

}

}

The PrintResult function propagates the values from internal nodes to the leaves and prints the final state of the array.

void PrintResult(int v, int lpos, int rpos)

{

if (lpos == rpos)

printf("%lld ", SegTree[v]);

else

{

int mid = (lpos + rpos) / 2;

Push(v, lpos, mid, rpos);

PrintResult(2 * v, lpos, mid);

PrintResult(2 * v + 1, mid + 1, rpos);

}

}

The main part of the program. Read the input data.

scanf("%d %d", &n, &m);

memset(SegTree,0,sizeof(SegTree));

Process m queries.

for(i = 0; i < m; i++)

{

scanf("%d %d %lld", &l, &r, &x);

Update(1,1,n,l,r,x);

}

Print the result.

PrintResult(1,1,n);

printf("\n");