7503. Олимпиада
На олимпиаду по
информатике прибыли n команд, в i-й команде ai (1 ≤ i
≤ n) участников. Для проведения соревнований подготовлены
классы, каждый из которых оснащён m компьютерами.
Определите
минимальное количество классов, которое необходимо задействовать, если в каждом
классе могут находиться только участники из разных команд. Иными словами, в
одном классе не должно быть более одного участника от каждой команды.
Вход. В первой строке заданы числа n и m. Во второй строке
содержатся n чисел ai (1 ≤ i
≤ n). Все значения целые,
неотрицательные и не превышают 100.
Выход. Выведите одно число – минимальное
необходимое количество классов.
|
Пример
входа |
Пример
выхода |
|
5 3 2 3 4 1 2 |
4 |
РЕШЕНИЕ
циклы
Анализ алгоритма
Всего на
соревнование прибыло s = ![]() участников. Поскольку каждая аудитория оснащена m компьютерами, потребуется как минимум ⌈s / m⌉ комнат.
участников. Поскольку каждая аудитория оснащена m компьютерами, потребуется как минимум ⌈s / m⌉ комнат.
Пусть p – наибольшее количество участников в одной команде (максимальное значение
среди всех чисел
ai). Если p > ⌈s / m⌉, то потребуется как минимум p комнат.
Конструктивно
можно показать, что всегда достаточно max(![]() , p) аудиторий для проведения олимпиады.
, p) аудиторий для проведения олимпиады.
Пример
На олимпиаду
прибыло 2 + 3 + 4 + 1 + 2 = 12 школьников. Так как каждый класс оснащён 3 компьютерами,
для проведения олимпиады потребуется как минимум 12 / 3 = 4 класса.
Наибольшее число
участников представляет третья команда – 4 человека. Их
можно рассадить по одному в разные 4 класса.
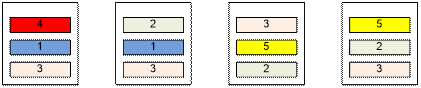
Например,
возможна следующая рассадка участников:
Реализация алгоритма
Читаем входные данные.
scanf("%d %d",&n,&m);
Вычисляем общее число участников s, а также размер p наибольшей команды.
p = 0;
for (i = 0; i < n; i++)
{
scanf("%d",&x);
s += x;
if (x > p) p = x;
}
Значение res =
⌈s /
m⌉
вычисляем как
(s + m – 1) / m.
res = (s + m -
1) / m;
Если p > ⌈s /
m⌉, то ответом будет
p.
if (res < p) res = p;
Выводим ответ.
printf("%d\n",res);