7503. Olympiad

At the Informatics Olympiad, n teams have arrived, with a_i (1 ≤ i ≤ n) participants in the i-th team. For the competition, classrooms have been prepared, each equipped with m computers.

Determine the minimum number of classrooms that must be used, given that each classroom may contain only participants from different teams. In other words, no classroom may have more than one participant from the same team.

Input. The first line contains two integers n and m. The second line contains n integers a_i (1 ≤ i ≤ n). All values are integers, non-negative, and do not exceed 100.

Output. Print one integer – the minimum required number of classrooms.

Sample input	Sample output
5 3 2 3 4 1 2	4

SOLUTION

loops

Algorithm analysis

A total of s = participants arrived at the competition. Since each classroom is equipped with m computers, at least ⌈s / m⌉ rooms are required.

Let p be the largest number of participants in a single team (the maximum among all values a_i). If p > ⌈s / m⌉, then at least p rooms are needed.

It can be shown constructively that it is always sufficient to have max(, p) classrooms to conduct the olympiad.

Example

A total of 2 + 3 + 4 + 1 + 2 = 12 students arrived at the olympiad. Since each classroom is equipped with 3 computers, at least 12 / 3 = 4 classrooms are required.

The largest team is the third one, with 4 participants. They can be seated one by one in 4 different classrooms.

For example, the following seating arrangement is possible:

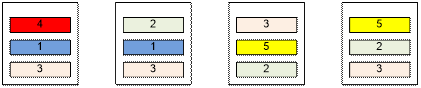
Algorithm implementation

Read the input data.

scanf("%d %d",&n,&m);

Compute the total number of participants s, as well as the size p of the largest team.

p = 0;

for (i = 0; i < n; i++)

{

scanf("%d",&x);

s += x;

if (x > p) p = x;

}

The value res = ⌈s / m⌉ is computed as (s + m – 1) / m.

res = (s + m - 1) / m;

If p > ⌈s / m⌉, then the answer is p.

if (res < p) res = p;

Print the answer.

printf("%d\n",res);