7531. Стационарная телефонная сеть
Мэр города RMR
хочет создать безопасную телефонную сеть для использования в экстренных
ситуациях в случае серьезных бедствий, когда город будет отрезан от внешнего
мира. Некоторые пары зданий в городе могут быть напрямую связаны телефонным
проводом. Инженеры муниципалитета подготовили оценку стоимости подключения
любой такой пары.
Мэр нуждается в
Вашей помощи – ему следует построить самую дешевую сеть, соединяющую все здания
в городе и удовлетворяющую мерам безопасности, которые изложены далее. Звонок
из здания A в другое здание B должен совершаться по простому пути (который не
содержит повторяющихся зданий). Существует несколько небезопасных зданий, в
которых живут люди с криминальной историей. Мэр хочет чтобы к этим зданиям был
только доступ из сети. То есть никакое соединение между зданиями A и B не
должно проходить через небезопасное здание C в сети (где C отлично от A и B).
Вход. Первая строка содержит три целых числа n, m,
p, где n (1 ≤ n ≤
1000) – количество
домов, m (0 ≤ m ≤ 105)
– количество
возможных прямых соединений между парами домов, а p (0 ≤ p ≤ n) – количество небезопасных зданий.
Здания пронумерованы от 1 до n.
Вторая строка содержит p различных
целых чисел от 1 до n (включительно) –
номера небезопасных зданий. Каждая из следующих m строк содержит три целых числа xi, yi
и li описывающих одну
потенциальную прямую линию, где xi
и yi (1 ≤ xi, yi ≤ n)
– различные номера зданий, которые она соединяет, а li (1 ≤ li
≤ 10000) – стоимость соединения этих зданий. Между любыми двумя городами
существует не более одного прямого соединения.
Выход. Выведите
стоимость самой дешевой сети, удовлетворяющей по возможности условиям
безопасности. Иначе выведите “impossible”.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 6 1 1 1 2 1 1 3 1 1 4 1 2 3 2 2 4 4 3 4 3 |
6 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
4 3 2 1 2 1 2 1 2 3 7 3 4 5 |
impossible |
РЕШЕНИЕ
графы –
минимальный остов – алгоритм Крускала
Анализ алгоритма
Найдем величину
минимального остова для всех зданий кроме небезопасных. Затем каждое
небезопасное здание подключим к ближайшему к нему безопасному. Искомую сеть построить
нельзя, если граф несвязный.
Отдельно следует
разобрать случай, когда в городе безопасных зданий нет. Если при этом имеется
только одно небезопасное здание, то ответ 0, если два – то ответ равен расстоянию
между ними. Если небезопасных зданий более 2, то искомой сети не существует.
Пример
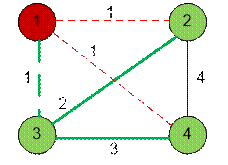
Рассмотрим первый пример. Небезопасный
дом имеет номер 1. Строим минимальный остов на вершинах 2, 3, 4 – его величина
равна 5. Подсоединяем к остову дом номер 1. Стоимость
самой дешевой сети равна 6.
Рассмотрим второй пример. Номера
небезопасных домов 1 и 2. Небезопасный дом номер 1 должен напрямую быть
подключен к безопасному, что для заданной сети невозможно. Поэтому ответ impossible.
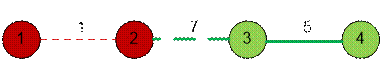
Реализация алгоритма
Объявим константу бесконечность INF. Ребра графа храним в
массиве v.
#define INF 1000000
struct Edge
{
int u,
v,dist;
Edge(int u, int v, int dist) :
u(u), v(v), dist(dist) {};
};
vector<Edge>
e;
Если u –
небезопасный дом, то danger[u] будет
хранить расстояние от него до ближайшего безопасного дома.
vector<int> danger;
Функция lt является компаратором для ребер графа.
int lt(Edge a, Edge b)
{
return
(a.dist < b.dist);
}
Основная часть программы. Читаем входные данные.
Инициализируем массив mas для системы непересекающихся множеств.
scanf("%d %d %d",&n,&m,&p);
mas.resize(n +
1);
for(i = 1; i <= n; i++) mas[i] = i;
Читаем небезопасные дома u.
danger.resize(n
+ 1);
for(i = 0; i < p; i++)
{
scanf("%d",&u);
danger[u] = INF;
}
Ищем кратчайшее расстояние от небезопасных домов до ближайших
безопасных. Пересчет совершаем для таких ребер (u, v), где одна вершина
принадлежит безопасному дому, а другая небезопасному.
for(i = 0; i < m; i++)
{
scanf("%d %d
%d",&u,&v,&dist);
if
((danger[u] > 0) && (danger[v] == 0))
danger[u] = min(danger[u],dist);
if
((danger[v] > 0) && (danger[u] == 0))
danger[v] = min(danger[v],dist);
Если обе вершины – безопасные дома, то добавляем
соответствующее ребро в граф.
if
((danger[u] == 0) && (danger[v] == 0))
e.push_back(Edge(u,v,dist));
}
Если граф не содержит ребер, то ответ 0.
if (m == 0)
{
puts("0");
return 0;
}
Если граф содержит одно ребро, соединяющее два дома (безопасных
или небезопасных), то выводим расстояние между ними.
if (m == 1)
{
printf("%d\n",dist);
return 0;
}
Сортируем ребра графа. Массив e хранит только ребра,
соединяющие безопасные дома.
sort(e.begin(),e.end(),lt);
Запускаем алгоритм Крускала. Ищем величину res минимального остова. В переменной cnt подсчитываем количество ребер в
построенной сети.
cnt = res = 0;
for(i = 0; i < e.size(); i++)
if
(Union(e[i].u,e[i].v))
{
res += e[i].dist;
cnt++;
}
Подсоединяем к минимальному остову небезопасные дома.
Прибавляем к res расстояния от них до
ближайших безопасных домов.
for (i = 1; i <= n; i++)
if (danger[i] > 0)
{
res += danger[i];
cnt++;
}
Если полученный граф не связный или величина полученной сети
больше бесконечности INF (например существует небезопасный дом, от которого нет
пути к остову), то ответ impossible.
Иначе выводим длину минимальной сети res.
if ((cnt != n - 1) || (res > INF))
puts("impossible");
else
printf("%d\n",res);
Java реализация
import java.util.*;
class Edge
{
int u, v, dist;
Edge (int u, int v, int dist)
{
this.u = u;
this.v = v;
this.dist = dist;
}
};
public class Main
{
static int mas[];
static int size[];
static int
Repr(int n)
{
while (n != mas[n]) n = mas[n];
return n;
}
static boolean
Union(int x,int y)
{
x = Repr(x);
y = Repr(y);
if (x == y) return false;
mas[y] = x;
return true;
}
public static class
MyFun implements Comparator<Edge>
{
public int compare(Edge
a, Edge b)
{
return a.dist - b.dist;
}
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
int p = con.nextInt();
mas = new int[n+1];
for(int i = 1;
i <= n; i++)
mas[i] = i;
int danger[] = new int[n+1];
for (int i = 0;
i < p; i++)
{
int u = con.nextInt();
danger[u] =
Integer.MAX_VALUE;
}
Vector<Edge> e = new
Vector<Edge>();
int dist = 0;
for(int i = 0;
i < m; i++)
{
int u = con.nextInt();
int v = con.nextInt();
dist = con.nextInt();
if ((danger[u]
> 0) && (danger[v] ==
0))
danger[u] =
Math.min(danger[u], dist);
if ((danger[v]
> 0) && (danger[u] ==
0))
danger[v] =
Math.min(danger[v], dist);
if ((danger[u] ==
0) && (danger[v] ==
0))
e.add(new
Edge(u, v, dist));
}
if (m ==
0)
{
System.out.println("0");
System.exit(0);
}
if (m ==
1)
{
System.out.println(dist);
System.exit(0);
}
Collections.sort(e, new
MyFun());
int cnt = 0;
long res = 0;
for (int i = 0;
i < e.size(); i++)
if (Union(e.get(i).u, e.get(i).v))
{
res += e.get(i).dist;
cnt++;
}
for (int i = 1;
i <= n; i++)
if (danger[i]
> 0)
{
res += danger[i];
cnt++;
}
if ((cnt != n - 1)
|| (res > Integer.MAX_VALUE))
System.out.println("impossible");
else
System.out.println(res);
con.close();
}
}