7534. Locked Treasure

A group of n bandits hid their stolen treasure in a room. The treasure needs to be locked away until there is a need to retrieve it. Since the bandits do not trust each other, they wanted to ensure that at least m of the bandits must agree in order to retrieve the treasure.

They have decided to place multiple locks on the door such that the door can be opened if and only if all the locks are opened. Each lock may have up to n keys, distributed to a subset of the bandits. A group of bandits can open a particular lock if and only if someone in the group has a key to that lock.

Given n and m, how many locks are needed such that if the keys to the locks are distributed to the bandits properly, then every group of bandits of size at least m can open all the locks, and no smaller group of bandits can open all the locks?

For example, if n = 3 and m = 2, only 3 locks are needed – keys to lock 1 can be given to bandits 1 and 2, keys to lock 2 can be given to bandits 1 and 3, and keys to lock 3 can be given to bandits 2 and 3. No single bandit can open all the locks, but any group of 2 bandits can open all the locks. You should also convince yourself that it is not possible to satisfy the requirements with only 2 locks.

Input. The first line contains the number of cases to follow. Each case is specified by the two integers n (1 ≤ n ≤ 30) and m (1 ≤ m ≤ n) on one line.

Output. For each line print on one line the minimum number of locks needed.

Sample input	Sample output
4 3 2 5 1 10 7 5 3	3 1 210 10

SOLUTION

combinatorics

Algorithm analysis

The minimum number of locks required equals to . Then any group of m bandits will be able to open the door (all locks), but no group of fewer bandits will be able to enter the room with the treasure.

Example

Let we have n = 4 bandits.

If m = 1, the number of locks equals to = 1. Each bandit must have one key from one lock:

If m = 2, the number of locks equals to = 4. The keys from locks 1, 2, 3, 4 should be distibuted among the bandits in the next way:

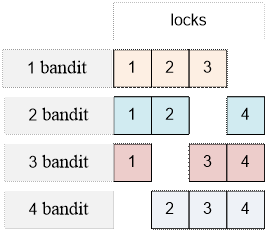
Any two bandits can open all four locks and take away the treasure.

If m = 3, the number of locks equals to = 6. The keys from locks 1, 2, 3, 4, 5, 6 should be distibuted among the bandits in the next way:

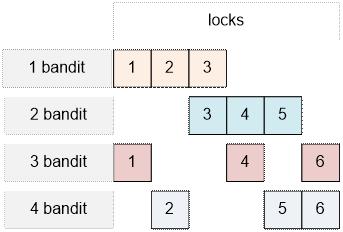
Any two bandits will not have a key from just one lock. Any three bandits will be able to open all six locks and pick up the treasure.

If m = 4, the number of locks equals to = 4. The keys from locks 1, 2, 3, 4 should be distibuted among the bandits in the next way:

In order to open all 4 locks, each bandit must bring his own unique key.

Consider the case n = 5, m = 3. Numer of locks equals to = 10. The optimal distribution of keys from locks among bandits is as follows:

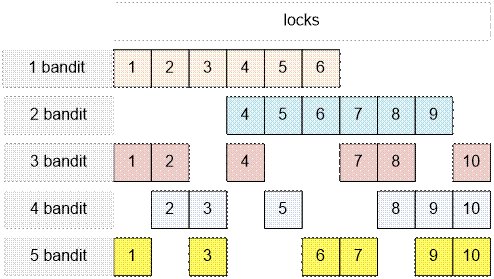
Algorithm realization

In the cells cnk[n][k] calculate the value of .

#define MAX 31

long long cnk[MAX][MAX];

Fill array cnk of binomial coefficients.

void FillCnk(void)

{

int n, k;

memset(cnk,0,sizeof(cnk));

for(n = 0; n < MAX; n++) cnk[n][0] = 1;

for(n = 1; n < MAX; n++)

for(k = 1; k <= MAX; k++)

cnk[n][k] = cnk[n-1][k] + cnk[n-1][k-1];

}

Main part of the program. Read input data and print the answer.

FillCnk();

scanf("%d",&tests);

while(tests--)

{

scanf("%d %d",&n,&m);

printf("%lld\n",cnk[n][m-1]);

}