7538. Flipping
Cards
Mike and his young
daughter Jesse are playing a new card game meant for kids. The rules are quite
simple, each player is dealt a hand of cards. Each card has one picture on each
side. They take turns playing cards and the first one to run out of cards is
the winner.
A player’s turn consists
of picking a subset of cards from their hand and laying them on the table. The
only rule is that the cards must be placed on the table such that no two cards
are showing the same picture.
Mike thought this was a
very appropriate game to play with his kid because of the simple rules. Mike
also liked this game because finding the best strategy is an algorithmically
interesting challenge!
Help Mike determine if he
can play his entire hand on his first round.
Input. The first line contains a single positive integer t (t
≤ 10) indicating the number of test cases. Each test case begins with a
single integer n (1 ≤ n ≤ 50 000) denoting the number of
cards in Mike's hand. Following this are n
lines, each describing a card in Mike’s hand.
The pictures on the cards are represented by integers. The i-th card is given by two integers pi, qi where 1 ≤ pi,
qi ≤ 2n.
Output. For each test case you
should output a single line with the word possible
if it is possible for Mike to play his entire hand in one turn, or impossible if Mike cannot play his
entire hand in one turn.
|
Sample
input |
Sample
output |
|
3 3 1 2 1 3 2 3 3 1 2 1 2 1 2 1 1 1 |
possible impossible possible |
SOLUTION
graphs
– cycles, DSU
Algorithm analysis
Each picture
depicted on the cards will be assigned one vertex of the graph. Each card will
be assigned an undirected edge (that connects the vertices corresponding to the pictures on the
sides of the card). The resulting graph may be disconnected.
The answer to
the problem will be possible if each connected component of the graph
contains at most one cycle. Finding the connected components and counting the number of cycles in them
can be done using a system
of disjoint sets.
Example
Consider four
cards. In yellow we denote the sides of the cards with which they will lie up.
Let’s mark the edge
of the graph with a picture with which the corresponding card will lie up.
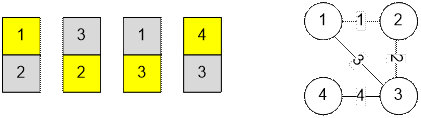
Consider the
case with two connected components:
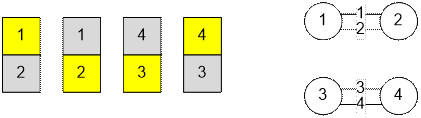
Algorithm realization
Define arrays for data processing. The dsu array is used for the
disjoint set system. If i is a representative of a set, then has_cycle[i]
contains information
about the number of cycles in it:
·
has_cycle[i] =
0, no cycles;
·
has_cycle[i] = 1,
one cycle;
·
has_cycle[i] > 1, more than one cycle;
#define MAX 50010
int dsu[2*MAX], has_cycle[2*MAX];
The function Repr returns a representative of
the set that contains vertex n.
int Repr(int n)
{
if (n == dsu[n])
return n;
return dsu[n]
= Repr(dsu[n]);
}
The function Union joins the sets containing the
vertices x and y.
void Union(int x, int y)
{
int x1 =
Repr(x), y1 = Repr(y);
If x and y already belong to the same connected
component (they have the same representative), and there is an edge (x, y),
then another cycle is formed. Add 1 to the number of cycles of their representative
(x1 is a representative of x and y).
if (x1 == y1)
has_cycle[x1]++;
If x and y belong to different connected
components, and y1 becomes
a representative of the set, then we add the number of cycles for x1 to the number of cycles for y1.
else
{
dsu[x1] = y1;
has_cycle[y1] += has_cycle[x1];
}
}
The main part of the program. Read the input data.
scanf("%d",&tests);
while (tests--)
{
scanf("%d",&n);
Initialize the system of disjoint sets.
for(i = 1; i <= 2*n; i++)
{
dsu[i] = i;
has_cycle[i] = 0;
}
Construct a system of disjoint sets.
for (i = 0; i < n; i++)
{
scanf("%d
%d",&p,&q);
Union(p,q);
}
Check if at least one connected component contains more than one cycle.
for (i = 1; i <= 2*n; i++)
if
(has_cycle[i] > 1) break;
Print the answer.
printf("%s\n",((i
<= 2 * n) ? "impossible" : "possible"));
}
Java realization
import java.util.*;
//import java.io.*;
public class Main
{
static int dsu[], has_cycle[];
static int Repr(int n)
{
if (n == dsu[n]) return n;
return dsu[n] = Repr(dsu[n]);
}
static void Union(int x, int y)
{
int x1 = Repr(x), y1 = Repr(y);
if (x1 == y1)
has_cycle[x1]++;
else
{
dsu[x1] = y1;
has_cycle[y1] += has_cycle[x1];
}
}
public static void main(String[] args) //throws IOException
{
Scanner con = new Scanner(System.in);
//Scanner con = new Scanner(new FileReader
("7538.in"));
int tests = con.nextInt();
while(tests-- > 0)
{
int i, n = con.nextInt();
dsu = new int[2*n+2];
has_cycle = new int[2*n+2];
for(i = 1; i <= 2*n; i++)
{
dsu[i] = i;
has_cycle[i] = 0;
}
for (i = 0; i < n; i++)
{
int p = con.nextInt();
int q = con.nextInt();
Union(p,q);
}
for (i = 1; i <= 2*n; i++)
if (has_cycle[i] > 1) break;
if (i <= 2 * n)
System.out.println("impossible");
else
System.out.println("possible");
}
con.close();
}
}