7561. Перестройка Офиса

Гаррисон и Андерсон работают в компании под названием “Перестройка Офиса”. В конкурирующих компаниях работники хотят изменить реальность, в этой компании они пытаются предсказать будущее.

Имеется большая квадратная доска n × n. Изначально каждая клетка (x, y) этой доски содержит значение x + y (1 ≤ x, y ≤ n). Офисные работники знают, что в будущем на доске будет производиться только два типа запросов:

“R r” – сумма всех значений в строке r, вывести результат и установить все значения в строке r равными нулю;

“C c” – сумма всех значений в столбце c, вывести результат и установить все значения в столбце c равными нулю.

Они предсказали запросы и ответы на них. Они хотят убедиться, что результаты предсказаны правильно. Помогите им вычислить результаты запросов.

Вход. Первая строка содержит два целых числа n и q (1 ≤ n ≤ 10⁶, 1 ≤ q ≤ 10⁵) – размер квадрата и количество запросов.

Каждая из следующих q строк содержит описание запроса. Запросов может быть или строка “R r” (1 ≤ r ≤ n) или “C c” (1 ≤ c ≤ n).

Выход. Выведите q строк. В i-ой строке выведите результат i-го запроса.

Пример входа	Пример выхода
3 7 R 2 C 3 R 2 R 1 C 2 C 1 R 3	12 10 0 5 5 4 0

РЕШЕНИЕ

структуры данных

Анализ алгоритма

Рассмотрим доску размера n = 4, заполненную числами:

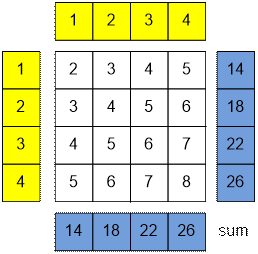
Справа указаны суммы по строкам, внизу – суммы по столбцам. Заметим, что суммы в соседних строках (и столбцах) отличаются на 4 – размер доски.

Найдем сумму чисел в строке row (1 ≤ row ≤ n). Она равна

(row + 1) + (row + 2) + … + (row + n) =

(1 + 2 + … + n) + n * row = + n * row

Заметим, что первое слагаемое суммы зависит только от размера n доски. Например, сумма чисел в третьей строке (row = 3) равна + 4 * 3 = 10 + 12 = 22.

Удалим из таблицы например второй столбец.

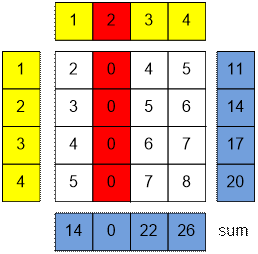
Теперь суммы в соседних строках отличаются на 3. При этом сумма чисел в строке row равна (row + 1) + (row + 3) + … + (row + n) = (1 + 3 + … + n) + (n – 1) * row. Из первого слагаемого суммы убрали 2, а множитель при row стал равным n – 1.

Аналогично можно утверждать, что если из таблицы удалили столбцы с номерами i₁, i₂, …, i_k (всего удалено k столбцов), то сумма чисел в строке row равна

(1 + 2 + … + n) – (i₁ + i₂ + … + i_k) + (n – k) * row

Например, если будут удалены все столбцы (k = n), то сумма чисел в любом ряду станет равной нулю.

Для решения задачи будем поддерживать множество удаленных строк и множество удаленных столбцов. Сначала эти множества пусты. Суммой строк будем называть число (1 + 2 + … + n) – (i₁ + i₂ + … + i_k), где i₁, i₂, …, i_k – номера уже удаленных столбцов. Будем также поддерживать две переменные – сумму строк Srow и сумму столбцов Scol.

Реализация алгоритма

Объявим множества удаленных строк и столбцов.

set<int> Row, Col;

Читаем размер квадрата n и количество запросов q.

scanf("%d %d\n",&n,&q);

Поскольку изначально все строки и столбцы присутствуют, то установим Srow = Scol = .

Srow = Scol = (n + 1LL) * n / 2;

Обрабатываем q запросов.

for(i = 0; i < q; i++)

{

scanf("%c %lld\n",&ch,&id);

Удаляем строку номер id.

if (ch == 'R')

{

Если строка номер id была удалена ранее (ее номер уже занесен во множество Row), то сумма чисел в ней равна нулю.

if (Row.find(id) != Row.end())

puts("0");

else

{

Заносим id во множество удаленных строк. Выводим ответ и пересчитываем Scol.

Row.insert(id);

printf("%lld\n",Srow + (n - Col.size()) * id);

Scol -= id;

}

}

else

Удаляем столбец номер id.

{

if (Col.find(id) != Col.end())

puts("0");

else

{

Col.insert(id);

printf("%lld\n",Scol + (n - Row.size()) * id);

Srow -= id;

}

}

}

Python реализация

Объявим множества удаленных строк и столбцов.

Row = set()

Col = set()

Читаем размер квадрата n и количество запросов q.

n, q = map(int, input().split())

Поскольку изначально все строки и столбцы присутствуют, то установим Srow = Scol = .

Srow = Scol = (n + 1) * n // 2

Обрабатываем q запросов.

for _ in range(q):

ch, id = input().split()

id = int(id)

Удаляем строку номер id.

if ch == 'R':

Если строка номер id была удалена ранее (ее номер уже занесен во множество Row), то сумма чисел в ней равна нулю.

if id in Row:

print("0")

else:

Заносим id во множество удаленных строк. Выводим ответ и пересчитываем Scol.

Row.add(id)

print(Srow + (n - len(Col)) * id)

Scol -= id

else:

Удаляем столбец номер id.

if id in Col:

print("0")

else:

Col.add(id)

print(Scol + (n - len(Row)) * id)

Srow -= id