7707. Охотник за головами II
Спайк – охотник за
головами – отслеживает преступника в космическом пространстве. К счастью для
него путешествия через гиперпространства сделало задачу посещения нескольких
планет намного проще. Каждая планета имеет ряд астральных ворот; каждые такие
ворота соединяется с воротами на другой планете. Эти соединения в
гиперпространстве по понятным причинам безопасности являются однонаправленными:
ворота с одной планеты являются точкой входа, а ворота с другой планеты –
точкой выхода из гиперпространства. Кроме того, сеть гиперпространственных
соединений не содержит петель, чтобы предотвратить астральный мир от взрыва –
все еще помнят трагический урок аварии ворот в 2022 году, когда была уничтожена
большая часть Луны.
Глядя на
звездную карту, Спайк задается вопросом: сколько друзей ему следует привести,
чтобы совершить поиск на каждой планете. Каждая планета должна быть посещена не
более чем одним другом, в противном случае преступник может что-то заподозрить
и бежать прежде чем его захватят в плен. Каждый человек может начать поиск на
любой планете по своему выбору и путешествовать по гиперпространственным
соединениям с одной планеты на другую, будучи связанным ограничениями на
количество гиперпространственных поездок.
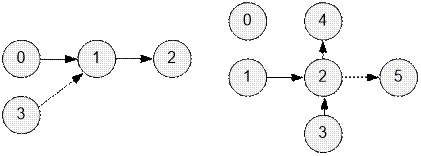
Вход. Начинается с целого числа n (0 < n ≤ 1000)
– количества планет. Планеты пронумерованы от 0 до n – 1. Следующие n строк
задают связи в гиперпространстве. i-ая
из этих строк содержит количество связей k
(0 ≤ k ≤ n – 1) исходящих из планеты i, за которым следует k целых чисел – планеты назначения.
Выход. Вывести
минимальное количество лиц, необходимых для посещения каждой планеты.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 1 1 1 2 0 1 1 |
2 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
6 0 1 2 2 4 5 1 2 0 0 |
4 |
РЕШЕНИЕ
графы -
паросочетания
Анализ алгоритма
Ориентированный
граф следует разбить на минимальное количество вершинно непересекающихся путей.
То есть эти пути должны покрывать все вершины.
Построим
двудольный граф (с долями OUT и IN). Множество OUT содержит вершины, из которых
выходят ребра. Множество IN содержит вершины, в которые входят ребра. Пусть m – максимальное паросочетание
построенного графа. Тогда ответом будет значение n – m.
Рассмотрим граф,
образованный ребрами паросочетания. Из каждой вершины исходит не более одного
ребра и в каждую вершину входит также не более одного ребра. То есть граф
представляет собой множество деревьев. Граф содержит n вершин и m ребер.
Следовательно в нем n – m компонент связности. Эти компоненты
связности и являются искомыми вершинно непересекающимися путями.
Пример
Различным
вариантам паросочетания будут соответствовать различные покрытия.
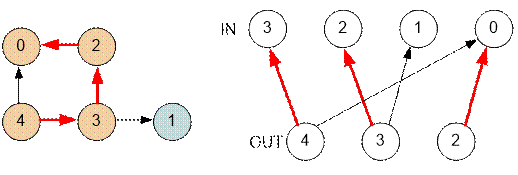
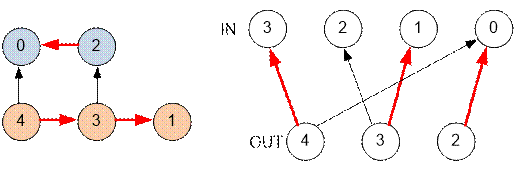
Реализация алгоритма
Объявим массивы для поиска максимального паросочетания.
vector<vector<int> > g;
vector<int> used, mt, par;
Поск в глубину из вершины v.
Ищем дополняющий путь.
int dfs(int
v)
{
if (used[v]) return 0;
used[v] = 1;
for (int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if (mt[to]
== -1 || dfs(mt[to]))
{
mt[to] = v;
par[v] = 1;
return 1;
}
}
return 0;
}
Поиск максимального паросочетания.
void AugmentingPath(void)
{
int i, run;
mt.assign (n, -1);
par.assign (n, -1);
for (run = 1;
run; )
{
run = 0; used.assign(n, 0);
for (i = 0;
i < n; i++)
if
((par[i] == -1) && dfs(i)) run = 1;
}
}
Основная часть программы. Читаем входные данные. Строим граф
g паросочетаний.
scanf("%d",&n);
g.resize(n+1);
for(i = 0; i < n; i++)
{
scanf("%d",&k);
g[i].assign(k,0);
for(j = 0; j
< k; j++)
scanf("%d",&g[i][j]);
}
Ищем максимальное паросочетание в переменной flow.
AugmentingPath();
for (flow = 0, i = 0; i < n; i++)
if (mt[i] !=
-1) flow++;
Выводим ответ.
printf("%d\n",n - flow);