7710. Изменение сценария
Каждый день Вы
едете на работу, используя дороги самого короткого пути. Это эффективно, но со
временем Вам надоедает смотреть на одни и те же здания и перекрестки каждый
день. Вы решаете искать другие маршруты. Конечно, Вы не хотите жертвовать
временем, так что новый путь должен быть столь же коротким, как и старый.
Существует ли другой путь, который отличается от старого, хотя бы одной улицей?
Вход. Первая строка содержит три числа n, m
и k (1 ≤ k ≤ n ≤ 104, 0 ≤ m ≤ 106), где n количество перекрестков, m количество улиц в городе, а k количество перекрестков которые Вы
проезжаете каждый день.
Следующая строка содержит k целых чисел – индексы (начиная с 1) перекрестков которые Вы
проезжаете каждый день. Первым перекрестком в этом списке всегда будет 1, а
последним всегда будет n. Это будет
именно кратчайший путь между 1 и n,
проходящий по k перекресткам.
Далее идут m
строк. i-ая строка содержит три целых
числа ai, bi, ci и описывают улицу от перекрестка ai до перекрестка bi
длиной ci (1 ≤ ai, bi ≤ n,
1 ≤ ci ≤ 104). Все улицы двунаправленные.
Между одной парой перекрестков может существовать
несколько улиц. Кратчайший путь для каждой соседней пары перекрестков a и b
использует улицу минимальной длины от a
до b.
Выход. Вывести “yes” если существует
другой путь такой же длины и “no” иначе.
|
Пример входа 1 |
Пример выхода 1 |
|
3 3 3 1 2 3 1 2 1 2 3 2 1 3 3 |
yes |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
4 5 2 1 4 1 2 2 2 4 1 1 3 1 3 4 2 1 4 2 |
no |
РЕШЕНИЕ
графы -
Дейкстра
Анализ алгоритма
Строка с k
перекрестками, которые Вы проезжаете каждый день, не несет никакой информации.
Пусть d – длина кратчайшего пути от между
вершинами 1 и n. В задаче требуется
установить, существует ли более одного пути длины d между вершинами 1 и n.
Запустим
алгоритм Дейкстры из 1 вершины. Заведем массив mult, в котором mult[i] = 1 если от начальной до i-ой вершины существует более одного
пути. Иначе положим mult[i] = 0.
Рассмотрим релаксацию ребра от v к to длины cost. Если dist[to] = dist[v] + cost, то существует
как минимум второй путь от начальной вершины к to. Устанавливаем mult[to] = 1. В случае же релаксации положим mult[to] = mult[v].
Между вершинами 1 и n существует более одного пути, если mult[n] = 1.
Пример
Графы,
приведенные в примерах, имеют следующий вид.
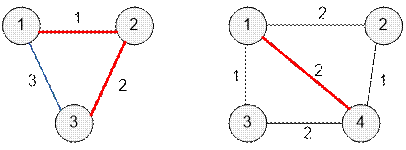
В первом тесте
имеется два пути кратчайшей длины 3 между вершинами 1 и 3. Во втором тесте
кратчайший путь между 1 и 4 равен 2. Второго пути длины 2 между вершинами 1 и 4
нет.
Реализация алгоритма
Объявим константу бесконечность oo и дополнительные
массивы.
#define oo 0x3F3F3F3F
vector<int> used, dist, mult;
Структура edge хранит
информацию о ребре: вершину node в которую оно
идет и его длину dist. Структура edge также будет
использована в очереди с приоритетами. Очередь хранит вершины графа, где
· node – номер вершины;
· dist – текущее расстояние от начальной вершины до
вершины node.
На вершине очереди
будет находиться вершина графа с наименьшим значением dist.
struct edge
{
int node,
dist;
edge(int
node, int dist) : node(node), dist(dist) {}
bool operator< (const
edge a) const
{
return dist
> a.dist;
}
};
Объявим список смежности графа g и очередь с приоритетами pq
для алгоритма Дейкстры.
vector<vector<edge>
> g;
priority_queue<edge>
pq;
Релаксация ребра идущего от v к to длины cost. Если dist[to] = dist[v] + cost, то
существует как минимум второй путь от начальной вершины к to.
Устанавливаем mult[to] = 1. В случае
релаксации существование более одного пути к v должно вести к существованию более одного пути к to, положим mult[to] = mult[v].
void
Relax(int v, int
to, int cost)
{
if (dist[to]
== dist[v] + cost)
mult[to] = 1;
if (dist[to]
> dist[v] + cost)
{
dist[to] = dist[v] + cost;
pq.push(edge(to,dist[to]));
mult[to] = mult[v];
}
}
Основная часть программы. Читаем входные данные.
Взвешенный граф храним в списке смежности g.
scanf("%d %d %d",&n,&m,&k);
for(i = 0; i < k; i++) scanf("%d",&temp);
g.resize(n+1);
for(i = 0; i < m; i++)
{
scanf("%d %d
%d",&a,&b,&w);
g[a].push_back(edge(b,w));
g[b].push_back(edge(a,w));
}
Инициализируем дополнительные массивы.
dist.assign(n+1,oo);
dist[1] = 0;
used.assign(n+1,0);
mult.assign(n+1,0);
Заносим первую вершину в очередь с приоритетами. Запускаем
алгоритм Дейкстры.
pq.push(edge(1,0));
while(!pq.empty())
{
edge e = pq.top(); pq.pop();
v = e.node;
Если извлеченная из очереди вершина фиктивна, то не
обрабатываем ее.
if (e.dist
> dist[v]) continue;
Перебираем и релаксируем ребра, смежные с вершиной v.
for(j = 0; j
< g[v].size(); j++)
{
to = g[v][j].node;
cost = g[v][j].dist;
if
(!used[to]) Relax(v,to,cost);
}
}
Выводим ответ в зависимости от значения mult[n].
if (mult[n] == 1)
puts("yes");
else
puts("no");
Java реализация
import java.util.*;
class Node implements Comparator<Node>
{
public int node, dist;
Node() {}
Node(int node, int dist)
{
this.node = node;
this.dist = dist;
}
@Override
public int compare(Node a, Node b)
{
return a.dist - b.dist;
}
};
public class Main
{
// Adjacency
list representation of the edges
static
ArrayList<ArrayList<Node> > g;
static int dist[], mult[];
static int INF = Integer.MAX_VALUE;
static int n, m, k;
static void dijkstra(int start)
{
PriorityQueue<Node> pq = new
PriorityQueue<Node>(n+1, new Node());
for (int i = 0; i <= n; i++)
dist[i] = Integer.MAX_VALUE;
// Add source
node to the priority queue
pq.add(new Node(start, 0));
// Distance to
the source is 0
dist[start] = 0;
while(!pq.isEmpty())
{
Node e = pq.poll();
int v = e.node;
if (e.dist > dist[v]) continue;
for(int j = 0; j < g.get(v).size(); j++)
{
int to = g.get(v).get(j).node;
int cost = g.get(v).get(j).dist;
if (dist[v] + cost == dist[to]) mult[to] = 1;
if (dist[v] + cost < dist[to])
{
dist[to] = dist[v] + cost;
pq.add(new Node(to,dist[to]));
mult[to] = mult[v];
}
}
}
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
k = con.nextInt();
for(int i = 0; i < k; i++)
con.nextInt();
g = new ArrayList<ArrayList<Node>
>();
// Initialize
list for every node
for (int i = 0; i <= n; i++)
{
ArrayList<Node> item = new
ArrayList<Node>();
g.add(item);
}
for(int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
int w = con.nextInt();
g.get(a).add(new Node(b,w));
g.get(b).add(new Node(a,w));
}
dist = new int[n+1];
mult = new int[n+1];
dijkstra(1);
if (mult[n] == 1)
System.out.println("yes");
else
System.out.println("no");
con.close();
}
}