7747. City Horizon

Farmer John has taken his cows on a trip to the city! As the sun sets, the cows gaze at the city horizon and observe the beautiful silhouettes formed by the rectangular buildings.

The entire horizon is represented by a number line with n (1 ≤ n ≤ 40000) buildings. Building i’s silhouette has a base that spans locations a_i through b_i along the horizon (1 ≤ a_i < b_i ≤ 10⁹) and has height h_i (1 ≤ h_i ≤ 10⁹). Determine the area, in square units, of the aggregate silhouette formed by all n buildings.

Input. The first line contains a single integer n. Each of the next n lines describes building i with three space-separated integers: a_i, b_i and h_i.

Output. Print the total area, in square units, of the silhouettes formed by all n buildings.

Sample input	Sample output
4 2 5 1 9 10 4 6 8 2 4 6 3	16

SOLUTION

sweeping line

Algorithm analysis

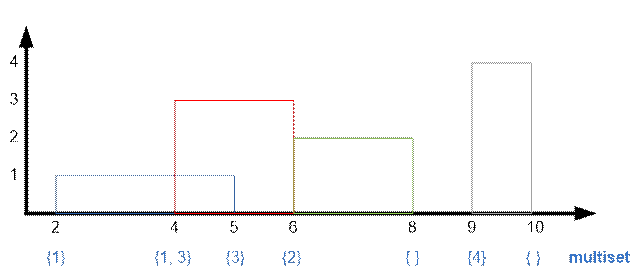
Let’s sort the points – the abscissas of the beginning and the end of buildings in ascending order. With each point store the information is it the beginning (type = 0) or the end (type = 1) of the building, as well as the building’s height. Sequentially process the points from left to right.

In the multiset s store the heights of buildings that have already started but are not finished yet. Maintain the heights in the multiset in descending order.

Let at the moment we are at the point x_i. Let h be the largest number in the multiset. This means that the current (at the interval [x_i, x_i+1]) tallest building has a height h (that is not finished yet). Add the value (x_i+1 – x_i) * h to the horizon area. If point x_i is the start of the building, then add the corresponding height to the multiset. If point x_i is the end of the building, then remove its height from the multiset. The order of processing the starts and the ends of the buildings with the same abscissas does not matter.

Example

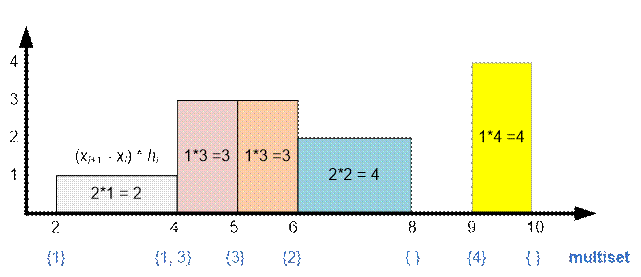
Algorithm realization

For a point, declare a structure node that will store its abscissa x, information is it the start (type = 0) or the end (type = 1) of the segment, as well as the height h of the corresponding building.

struct node

{

int x, type, h;

node(int x, int type, int h) : x(x), type(type), h(h) {};

};

Define a comparator f for points – we’ll sort them by abscissas.

int f(node a, node b)

{

return a.x < b.x;

}

Declare an array of points Event, as well as a multiset s for storing the heights of buildings intersecting with the current abscissa of the sweeping line.

vector<node> Event;

multiset<int, greater<int> > s;

Read the input data. Construct an array of points.

scanf("%d",&n);

for(i = 0; i < n; i++)

{

scanf("%d %d %d",&left,&right,&height);

Event.push_back(node(left,0,height));

Event.push_back(node(right,1,height));

}

Sort the array of points by non decreasing abscissas.

sort(Event.begin(),Event.end(),f);

In the variable res, compute the total area of the city silhouette.

res = 0;

Move from left to right along the points of the Event array. For each i value of the for loop, consider the interval (Event[i].x, Event[i + 1].x).

for (i = 0; i < Event.size() - 1; i++)

{

If point x_i is the start of the building, then add the corresponding height to the multiset.

int h = Event[i].h;

if (Event[i].type == 0) s.insert(h);

If point x_i is the end of the building, then remove the corresponding height from the multiset.

else s.erase(s.find(h));

If stack is not empty, then between the points Event[i].x and Event[i + 1].x there is a horizon line which height equals to the largest value in the multiset s, namely the value *s.begin ().

if (!s.empty())

res += 1LL * *s.begin() * (Event[i+1].x - Event[i].x);

}

Print the final area.

printf("%lld\n",res);

Algorithm realization – segment tree

Let’s compress the abscissas of the buildings using the map mp (mp[2] = 1, mp[4] = 2, and so on). Build a segment tree [1..len], where len ≤ 40000.

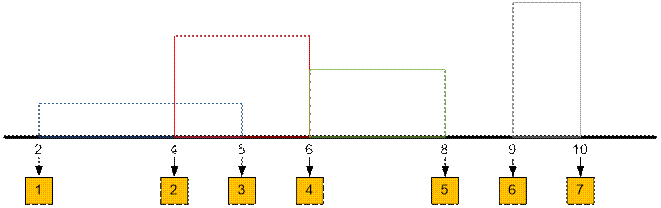
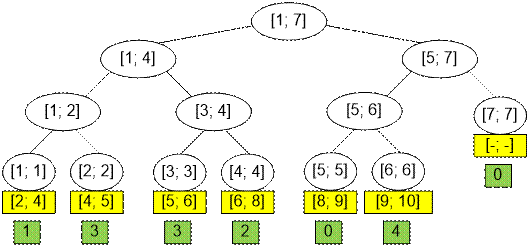
Each leaf of a segment tree corresponds to one indivisible interval silhouette of a horizon. For example, vertex 1 corresponds to the interval [2; 4], vertex 2 corresponds to the interval [4; 5]. Then segment [a, b] is covered by the vertices [mp[a], mp[b] – 1] of a segment tree. For example, the segment [2; 5] is covered by the vertices [mp[2], mp [5] – 1] = [1, 2].

For each building on the segment [a_i, b_i] of height h_i, increase by h_i all values of the segment tree on the interval [mp[a_i], mp[b_i] – 1]. When pushing the value at the vertex, maintain the maximum:

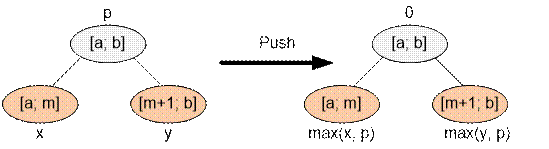
Let’s push all the vertex values to the leaves, after which the leaves will contain the silhouette heights at the intervals. For example, the first leaf corresponds to the segment [2; 4] and contains the value 1, the second leaf corresponds to the segment [4; 5] and contains the value 3, and so on. The last node of the segment tree does not correspond to any interval and is fictitious.

#include <cstdio>

#include <cstring>

#include <set>

#include <map>

#include <vector>

#include <algorithm>

#define MAX 80010

using namespace std;

int SegTree[4*MAX];

vector<int> a;

map<int,int> mp;

int i, n, l, r, h, len;

long long res;

struct Building

{

int left, right, height;

} b[40010];

void Push(int Vertex, int LeftPos, int Middle, int RightPos)

{

if (SegTree[Vertex])

{

SegTree[2*Vertex] = max(SegTree[2*Vertex],SegTree[Vertex]);

SegTree[2*Vertex+1] = max(SegTree[2*Vertex+1],SegTree[Vertex]);

SegTree[Vertex] = 0;

}

}

void Add(int Vertex, int LeftPos, int RightPos,

int Left, int Right, int x)

{

if (Left > Right) return;

if ((LeftPos == Left) && (RightPos == Right))

SegTree[Vertex] = max(SegTree[Vertex],x);

else

{

int Middle = (LeftPos + RightPos) / 2;

Push(Vertex,LeftPos,Middle,RightPos);

Add(2*Vertex, LeftPos, Middle, Left, min(Middle,Right), x);

Add(2*Vertex+1, Middle+1, RightPos, max(Left,Middle+1), Right, x);

}

}

long long Count(int Vertex, int LeftPos, int RightPos)

{

if (LeftPos == RightPos)

return 1LL * SegTree[Vertex] * (a[LeftPos+1] - a[LeftPos]);

else

{

int Middle = (LeftPos + RightPos) / 2;

Push(Vertex,LeftPos,Middle,RightPos);

return Count(2*Vertex, LeftPos, Middle) +

Count(2*Vertex+1, Middle+1, RightPos);

}

}

int main(void)

{

scanf("%d",&n);

memset(SegTree,0,sizeof(SegTree));

set<int> s;

for(i = 1; i <= n; i++)

{

scanf("%d %d %d",&b[i].left,&b[i].right,&b[i].height);

s.insert(b[i].left); s.insert(b[i].right);

}

len = s.size(); a.resize(len+2);

copy(s.begin(),s.end(),a.begin()+1);

for(i = 1; i <= len; i++) mp[a[i]] = i;

for(i = 1; i <= n; i++)

Add(1,1,len,mp[b[i].left],mp[b[i].right]-1,b[i].height);

res = Count(1,1,len);

printf("%lld\n",res);

return 0;

}