7757. Квадрат
У Джан-Джи
имеется кусок металла, из которого он хочет вырезать квадрат. Кусок состоит из
сетки n на n, которую Джан-Джи может разрезать только по границам сетки.
Каждая ячейка сетки либо исправная либо дефектная, при этом Джан-Джи хочет вырезать
наибольший квадрат, не содержащий дефектных клеток. После определения
максимального размера квадрата Джан-Джи хочет узнать сколькими различными
способами он может вырезать его из имеющегося куска. После чего Джан-Джи
следует вывести произведение максимального размера на количество способов
расположения наибольшего квадрата.
Рассмотрим кусок
материала размера 6 на 6. Черные ячейки дефектные. Наибольший квадрат, который
может вырезать Джан-Джи, имеет размер 3 на 3, причем имеется два варианта его
вырезать – красный и зеленый квадраты. Джан-Джи выведет произведение 3 и 2, то
есть 6.

Вам следует
найти размер наибольшего квадрата, который можно вырезать из куска материала, а
также посчитать, сколькими различными вариантами это можно сделать. После чего
вывести их произведение.
Вход. Первая строка содержит размер материала n (1 ≤ n ≤ 1000). Каждая из следующих n строк содержит n целых
чисел. 1 означает что участок сетки целый, а 0 означает что участок сетки
поврежден.
Выход. Вывести одно
число – произведение размера наибольшего квадрата в материале на количество
возможных его расположений в материале.
|
Пример
входа 1 |
Пример
выхода 1 |
|
6 1 0 1 0 1 0 0 1 0 1 0 1 1 0 1 0 1 0 0 1 0 1 0 1 1 0 1 0 1 0 0 1 0 1 0 1 |
18 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
6 0 1 1 1 1 0 1 0 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 1 1 1 1 0 1 1 1 0 1 1 1 |
6 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Заведем массив dp, где dp[i][j] хранит размер наибольшего квадрата,
который можно вырезать из прямоугольника (0, 0) – (i, j) при условии, что
этому наибольшему квадрату принадлежит ячейка (i, j).
Пусть массив m содержит входной участок.
Если m[i][j] = 0 (участок сетки поврежден), то dp[i][j]
= 0.
Пусть m[i][j]
= 1. Рассмотрим два случая:
1.
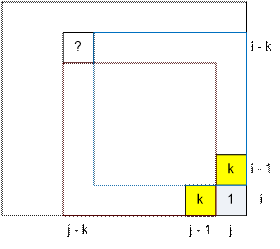
m[i – 1][j] = m[i][j – 1] = k. Тогда dp[i][j] зависит от значения
ячейки m[i – k][j – k]:
·
если m[i – k][j
– k] = 1, то весь квадрат (i – k,
j – k) – (i, j) будет содержать только единицы и dp[i][j]
= k + 1.
·
если m[i – k][j
– k] = 0, то dp[i][j] = k.
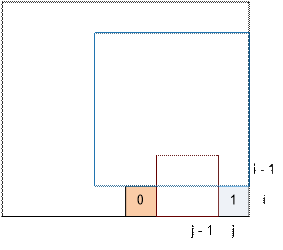
2. m[i – 1][j] ≠ m[i][j – 1]. Тогда dp[i][j] = min(dp[i – 1][j], dp[i][j – 1]) + 1.
Суммируя выше сказанное
можно заметить, что
dp[i][j]
= min(dp[i – 1][j], dp[i][j – 1], dp[i – 1][j – 1]) + 1
Рассмотрим второй тест. Заполним для него массив dp.
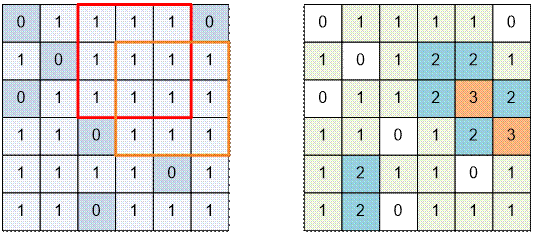
Имеется 2 наибольших квадрата размером 3 * 3. Произведение
размера наибольшего квадрата на количество его расположений равно 3 * 2 = 6.
Реализация алгоритма
Объявим рабочий массив dp.
#define MAX 1010
int dp[MAX][MAX];
Читаем значение n. Переменная size хранит размер наибольшего квадрата, cnt – количество раз, которое он встречается в куске. Инициализируем массив dp нулями.
scanf("%d", &n);
memset(dp,0,sizeof(dp));
size = cnt = 0;
Пересчитываем
массив dp по возрастанию строк, ячейки в каждой строке – по возрастанию
столбцов.
for(i = 1; i
<= n; i++)
for(j = 1; j
<= n; j++)
{
scanf("%d",&val);
Пусть все значения массива dp до клетки (i, j) уже посчитаны.
Читаем очередное значение val = m[i][j]
(входную матрицу в памяти не держим, читаем и обрабатываем ее на лету).
Поскольку изначально мы обнулили массив dp, то при val = 0 значение dp[i][j] будет оставаться равным 0.
if (val ==
1)
{
dp[i][j] = min(min(dp[i][j-1],dp[i-1][j]),dp[i-1][j-1])
+ 1;
Пересчитываем значения size и cnt для очередного квадрата размером dp[i][j].
if
(dp[i][j] == size) cnt++;
if
(dp[i][j] > size) {size = dp[i][j]; cnt = 1;}
}
}
Выводим ответ.
printf("%lld\n",1LL * size * cnt);