7784. Bars of gold
The highwaymen John
and Bob robbed the caravan and got as a target three gold bars. They decided to
divide the plunder like brothers. John and Bob weighed bars and found that they
weigh x1, x2 and x3
pounds respectively.
Now John and Bob
want to divide the bars so that each of them has got an equal amount of gold.
They do not want to cut the bars, but nowhere to go. After discussing the
situation, they decided that if they can, they will share the plunder as it is,
and if not, they will saw only one bar into two parts. To saw two or all three
bars of gold they can't.
Help John and Bob
to choose the bar to saw into two parts, and the sizes of these parts, so that
after cutting they can divide gold equally.
Input. One line contains
three integers: x1, x2 and x3
(1 ≤ xi ≤ 108, the sum of bar’s
weights is even).
Output. If it is not
possible to saw one bar so that to divide gold equally, print -1.
If John and Bob can
divide the gold equally without sawing, print 0.
Otherwise print on
the first line number 1, if they need to saw the first bar, 2 if they need to
saw the second bar, 3 if they need to saw the third bar. On the second line
print two positive integers: the weights of the parts into which the bar must
be sawn. These parts in the sum must give the weight of original bar. The total
weight of gold is even, so if the bar is cut, its parts have integers weight.
If some solutions exist, print any.
|
Sample input |
Sample output |
|
2 3 3 |
2 2 1 |
SOLUTION
mathematics
Algorithm analysis
First, let’s check
whether it is possible to separate the ingots without cutting. This is true if
one of the conditions holds: x1 + x2
= x3, x2 + x3 = x1 or x1 + x3
= x2.
Let’s add
three bars together (the order doesn’t matter).
Each of the robbers must receive mid = (x1
+ x2 + x3) / 2 gold. According to the
conditions of the problem, the sum of the weights of the bars is even, therefore mid is an integer.
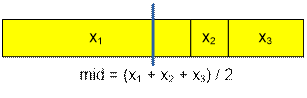
It is
always possible to divide gold with one cut. It remains to determine the piece
and into what parts it should be divided.
·
If mid < x1, then the
first piece should be divided into parts mid and x1 – mid.
·
If x1 < mid < x1 + x2, then the
second piece should be divided into parts mid – x1 and x1 + x2 – mid.
·
If x1 + x2 < mid, then the third piece
should be divided into parts mid – x1 – x2 and mid.
Algorithm realization
Read
the input data. Find the amount of gold mid that each of the robbers should receive.
scanf("%d %d %d",&a,&b,&c);
mid = (a + b + c) / 2;
Check if the gold can be divided without cutting.
if (a + b == mid || a + c == mid || b + c == mid)
{
puts("0");
return 0;
}
If
you need to cut the first piece.
if (mid < a)
{
printf("1\n%d %d\n",mid,a - mid);
return 0;
}
If
you need to cut the second piece.
if (mid < a + b)
{
printf("2\n%d %d\n",mid - a,a + b - mid);
return 0;
}
If
you need to cut the third piece.
printf("3\n%d %d\n",mid
- a - b,mid);