7807. Счастливая
сумма
Известно, что счастливым является число, десятичная
запись которого содержит только четверки и семерки. Например, счастливыми
являются числа 4, 7, 47, 7777 и 4744474.
Пусть S – множество счастливых чисел, не
меньших a и не
больших b:
S = {n : a ≤ n ≤ b, n – счастливое число}
Вычислите остаток от деления
на 1234567891 такой суммы:
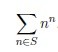
Вход. Два целых числа a и b (1 ≤ a ≤ b ≤ 1018).
Выход. Выведите остаток от деления счастливой суммы
на 1234567891.
Пояснение. 44 + 77 = 823799.
|
Пример входа |
Пример выхода |
|
1 10 |
823799 |
РЕШЕНИЕ
перебор + возведение в
степень
Анализ алгоритма
Модуль
p = 1234567891 простой. Следовательно np – 1 = 1 (mod p). Откуда
nn (mod p) = (n mod p)
(p – 1) + … + (p
– 1) + (n mod (p – 1)) (mod p) =
(n mod p) n mod (p – 1) (mod p)
Например
2323 (mod 5) = (23 mod 5) 4 + 4 + 4 + 4 + 4 + 3 (mod 5) = 33 (mod 5), так как 34 (mod 5) = 1.
Пусть
modPow(a, n) = an
mod p. Поскольку n ≤ 1018, то аргументами modPow(n, n) будет тип long long и при умножении получим
переполнение. Из выше приведенного равенства имеем:
modPow(n, n) = modPow(n mod p, n mod (p – 1))
Теперь
функции modPow передаются числа типа int.
Для
генерации счастливых чисел следует заметить, что если n – счастливое число, то таковыми являются 10*n + 4 и 10*n + 7.
Реализация алгоритма
Определим модуль MOD = 1234567891.
#define MOD 1234567891
Функция modPow вычисляет значение степени an по модулю MOD.
long long modPow(long long a, long long n)
{
if (n == 0) return 1;
if (n % 2 == 0) return modPow((a * a) % MOD, n / 2);
return (modPow(a, n - 1) * a) % MOD;
}
Рекурсивная генерация счастливых чисел.
void f(long long n)
{
Как только очередное сгенерированное число n станет больше b, останавливаем генерацию чисел.
if (n > b) return;
Суммируем nn только для тех счастливых чисел n, для которых a ≤ n ≤ b.
if (n >= a) res = (res + modPow(n % MOD, n % (MOD - 1))) % MOD;
Если
n – счастливое число, то таковыми являются 10*n + 4 и 10*n + 7.
f(n * 10 + 4);
f(n * 10 + 7);
}
Основная часть програмы. Читаем входные данные.
scanf("%lld %lld", &a, &b);
res = 0;
Генерируем счастливые числа, начиная с 0. Вычисляем
требуемую сумму в переменной res.
f(0);
Выводим ответ.
printf("%lld\n", res);