750. Домой на электричках
Одна из
команд-участниц олимпиады решила вернуться домой на электричках. При этом
ребята хотят попасть домой как можно раньше. К сожалению, не все электрички
идут от города, где проводится олимпиада, до станции, на которой живут ребята.
И, что еще более обидно, не все электрички, которые идут мимо их станции,
останавливаются на ней (равно как вообще, электрички останавливаются далеко не
на всех станциях, мимо которых они идут).
Все станции на
линии пронумерованы числами от 1 до n. При этом станция номер 1
находится в городе, где проводится олимпиада, и в момент времени 0 ребята
приходят на станцию. Станция, на которую нужно попасть ребятам, имеет номер e.
Напишите
программу, которая по данному расписанию движения электричек вычисляет
минимальное время, когда ребята могут оказаться дома.
Вход. Сначала записаны числа n (2 ≤ n
≤ 100) и e (2 ≤ e ≤ n). Затем записано
число m (0 ≤ m ≤ 100), обозначающее число рейсов
электричек. Далее идет описание m рейсов электричек. Описание каждого рейса
электрички начинается с числа ki (2 ≤ ki
≤ n) – количества станций, на которых она останавливается, а далее
следует ki пар чисел, первое число каждой пары задает номер
станции, второе – время, когда электричка останавливается на этой станции
(время выражается целым числом из диапазона от 0 до 109). Станции
внутри одного рейса упорядочены в порядке возрастания времени. В течение одного
рейса электричка все время движется в одном направлении - либо от города, либо
к городу.
Выход. Выведите одно
число – минимальное время, через которое ребята смогут оказаться на своей
станции. Если существующими рейсами электричек они добраться не смогут,
выведите -1.
|
Пример
входа |
Пример
выхода |
|
5 3 4 2 1 5 2 10 2 2 10 4 15 4 5 0 4 17 3
20 2 35 3 1 2 3 40 4 45 |
20 |
РЕШЕНИЕ
графы – алгоритм Дейкстры
Анализ алгоритма
Построим граф, количество вершин которого равно числу
станций. Каждое ребро графа соответствует перемещению одной электрички между
соседними станциями, на которых она останавливается. Если стартовав со станции i
в момент времени From, электричка приезжает на соседнюю станцию j
в момент времени To, то проведем от i до j ориентированное
ребро, записав на нем пару чисел (From, To). Граф будем задавать
списком смежности, поэтому каждому ребру следует еще приписать номер вершины,
куда оно направлено.
Запускаем алгоритм Дейкстры на построенном ориентированном
графе. Ищем кратчайший путь от вершины 1 до
вершины e.
Пример
Имеется пять станций и расписание движения четырех
электричек.
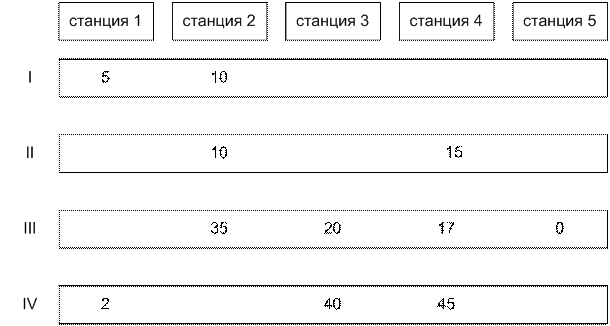
Соответствующий
граф имеет вид:
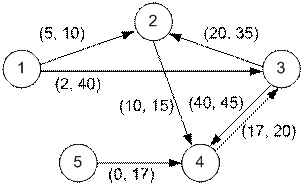
Реализация алгоритма
Алгоритм
Дейкстры реализуем при помощи очереди с приоритетами. Элементами очереди будут
пары (время за которое можно добраться от истока, номер вершины).
Таким образом, первой в очереди всегда будет вершина, в которую мы раньше всего
доберемся от истока (стартовая вершина, из которой запускается алгоритм
Дейкстры). Объявим класс Prior, содержащий эту пару (Time, Vertex).
Переопределим операторы сравнения меньше и больше: та пара считается меньшей, у
которой расстояние до истока Dist меньше.
class Prior
{
public:
int Time,
Vertex;
Prior(int
Time, int Vertex) : Time(Time), Vertex(Vertex)
{}
int operator< (const
Prior &a) const
{
return Time
< a.Time;
}
int operator> (const
Prior &a) const
{
return Time
> a.Time;
}
};
Объявим класс
ребро, соединяющие две соседние станции. Оно содержит следующие атрибуты:
·
vTo – номер станции, куда едет электричка;
·
timeFrom – время отправления электрички из текущей станции;
·
timeTo – время прибытия электрички на станцию vTo;
class Edge
{
public:
int vTo,
timeFrom, timeTo;
Edge(int vTo,
int timeFrom, int
timeTo)
: vTo(vTo), timeFrom(timeFrom),
timeTo(timeTo) {}
};
Объявим класс
граф. Он содержит количество вершин n и задается списком смежности g.
class Graph
{
public:
int n;
vector<vector<Edge> > g;
Graph(int n =
1) : n(n)
{
g = vector<vector<Edge> >(n);
}
Функция добавления ориентированного
ребра (From, To). Электричка выезжает со станции From в
момент времени timeFrom и
прибывает на станцию To в момент времени timeTo.
void AddEdge(int From, int To, int timeFrom, int
timeTo)
{
g[From].push_back(Edge(To,timeFrom,timeTo));
}
Алгоритм Дейкстры запускается из
вершины Source. Вторым аргументом передается массив time: time[i]
содержит наименьшее время, за которое можно добраться на электричках из вершины
Source в i.
void
Dijkstra(int Source, vector<int> &time)
{
priority_queue<Prior,
vector<Prior>, greater<Prior> > pq;
Кладем в очередь
пару (0, Source), полагаем время time[Source] равным 0 (добраться
от вершины Source до ее же самой можно за нулевое время).
pq.push(Prior(0,Source)); time[Source] = 0;
while(!pq.empty())
{
int v =
pq.top().Vertex;
int d =
pq.top().Time; pq.pop();
Проверяем, не является ли извлеченная
из головы очереди пара (v, d) фиктивной.
if (d
> time[v]) continue;
Просматриваем вершины to,
смежные с v. Пробуем провести релаксацию ребра (v, to).
for(int i = 0; i < g[v].size(); i++)
{
time[v] содержит наименьшее
время, за которое можно доехать до станции v. Если ребро (v, to)
содержит информацию, что электричка выезжает из v в to раньше,
чем time[v], то мы на эту электричку не успеваем.
if
(g[v][i].timeFrom < time[v]) continue;
Вычисляем станцию to, в
которое ведет ребро.
int to
= g[v][i].vTo ;
Если до станции to по ребру (v,
to) можно добраться за меньшее время, нежели уже имеется в time[to],
то проводим релаксацию и заносим пару (time[to], to) в очередь.
if
(time[to] > g[v][i].timeTo)
{
time[to] = g[v][i].timeTo;
pq.push(Prior(time[to],to));
}
}
}
}
};
Объявим
указатель на граф.
Graph *g;
Основная часть
программы. Инициализируем массив time, содержащий кратчайшее время, за которое
можно добраться до всех станций из начальной.
scanf("%d %d %d",&n,&e,&m);
g = new Graph(n+1);
time =
vector<int>(n+1,INF);
Читаем входные данные. Строим граф g.
for(i = 0; i < m; i++)
{
scanf("%d",&stations);
PrevStation = -1;
for(j = 0; j
< stations; j++)
{
scanf("%d
%d",&CurStation,&CurTime);
Электричка выезжает со станции PrevStation
в момент времени PrevTime и движется на следующую станцию CurStation,
на которую прибывает в момент времени CurTime.
if
(PrevStation != -1) g->AddEdge(PrevStation,CurStation,
PrevTime,CurTime);
PrevStation = CurStation; PrevTime =
CurTime;
}
}
Запускаем алгоритм Дейкстры из
вершины 1.
g->Dijkstra(1,time);
Выводим ответ.
if (time[e] == INF) printf("-1\n");
else printf("%d\n",time[e]);