750. Elektrik qatarları ilə evə

Olimpiada iştirakçı-komandalardan biri evə elektrik qatarı ilə qayıtmaq qərarına gəldi. Bu zaman uşaqlar evə mümkün qədər tez çatmaq istəyirlər. Təəssüf ki, heç də bütün qatarlar olimpiadanın keçirildiyi şəhərdən uşaqların yaşadıqları stansiyaya qədər getmir. Daha təəssüf doğuran odur ki, heç də bütün qatarlar onların stansiyasından keçərkən orada dayanmır (ümumiyyətlə, qatarlar yanından keçdikləri stansiyaların heç də hamısının uzaqlığında dayanmırlar).

Xətdəki bütün stansiyalar 1-dən N-ə qədər nömrələnmişdir. Bu zaman 1 nömrəli stansiya olimpiadanın olduğu şəhərdə yerləşir və 0 zamanında uşaqlar stansiyaya gəlirlər. Uşaqların gəlmək istədikləri stansiyanın nömrəsi E-dir.

Elektrik qatarlarının verilmiş hərəkət qrafikinə görə uşaqların evə çata biləcəkləri minimal zamanı hesablayan proqramı tərtib edin.

Giriş verilənləri. Giriş faylında əvvəlcə N (2 ≤ N ≤ 100) və E (2 ≤ E ≤ N) ədədləri verilir. Sonra qatarların reyslərinin sayını ifadə edən M (0 ≤ M ≤ 100) ədədi verilir. Daha sonra qatarların M reysinin təsviri verilir. Qatarın hər bir reysinin təsviri onun dayandığı stansiyaların sayını ifadə edən Ki (2 ≤ Ki ≤ N) ədədi ilə başlayır, daha sonra Ki ədəd cütlüyü verilir, hər bir cütlüyün birinci ədədi stansiyanın nömrəsini, ikincisi — qatarın bu stansiyada dayanacağı zamanı (zaman 0-dan 10⁹-a qədər 10 tam ədədlə verilir) ifadə edir. Bir reys daxilində stansiyalar zamana görə artan sıra ilə sıralanmışdır. Bir reys ərzində qatar həmişə bir istiqamətdə hərəkət edir – ya şəhərdən, ya da şəhərə doğru.

Çıxış verilənləri. Çıxış faylına yeganə ədədi — uşaqların öz stansiyalarına çata biləcəkləri minimal zamanı verin. Əgər qatarların mövcud reysləri ilə onlar evə çata bilməyəcəklərsə, –1 verin.

Giriş verilənlərinə nümunə

5 3

4

2 1 5 2 10

2 2 10 4 15

4 5 0 4 17 3 20 2 35

3 1 2 3 40 4 45

Çıxış verilənlərinə nümunə

20

HƏLLİ

qraflar – Dijkstra alqoritmi

Alqoritmin analizi

Təpələrinin sayı stansiyaların sayına bərabər olan qraf quraq. Qrafın hər bir tili bir qatarın dayandığı qonşu stansiyalar arasındakı hərəkətinə uyğundur. Əgər From anında i stansiyasından hərəkətə başlanılarsa, qatar qonşu j stansiyasına To anında çatmış olur, onda i-dən j-yə üzərində bir cüt ədəd (From, To) yazılmış istiqamətlənmiş til keçirək. Qrafı qonşuluq siyahısı şəklində verəcəyik, buna görə də hər bir til üçün onun istiqamətləndiyi təpənin nömrəsini də yazmaq lazımdır.

Qurulmuş istiqamətlənmiş qrafda Dijkstra alqoritmini icra edək. 1 təpəsindən e təpəsinə ən qısa yolu tapırıq.

Misal

Beş stansiya və dörd elektrik qatarının hərəkət qrafiki verilir.

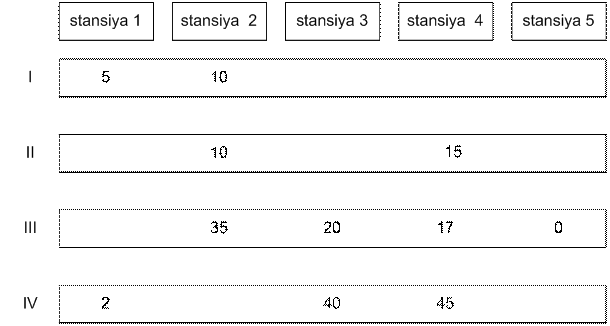
Uyğun qraf aşağıdakı formadadır:

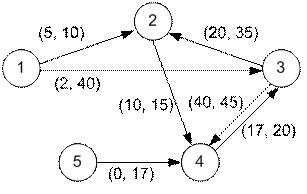
Alqoritmin reallaşdırılması

Dijkstra alqoritmini prioritetli növbə vasitəsilə reallaşdırırıq. Növbənin elementləri cütlüklərdir (mənbədən məntəqəyə çatmaq üçün zaman və təpənin nömrəsi). Beləliklə, növbədə birinci olaraq həmişə mənbədən (Dijkstra alqoritminin icra ediləcəyi başlanğıc təpədən) çatacağımız ilk təpə olacaq. Bu cütlüyü (Time, Vertex) ehtiva edən Prior sinfini elan edək. Böyük və kiçik operatorlarını təyin edək: o cütlük kiçik sayılır ki, mənbəyə qədər olan məsafə (Dist) ən kiçik olsun.

class Prior

{

public:

int Time, Vertex;

Prior(int Time, int Vertex) : Time(Time), Vertex(Vertex) {}

int operator< (const Prior &a) const

{

return Time < a.Time;

}

int operator> (const Prior &a) const

{

return Time > a.Time;

}

};

İki qonşu stansiyanı birləşdirən til sinfini elan edək. O növbəti atributları ehtiva edir:

· vTo – qatarın getdiyi stansiyanın nömrəsi;

· timeFrom – cari stansiyadan qatarın yola düşdüyü vaxt;

· timeTo – qatarın vTo stansiyasını çatdığı vaxt;

class Edge

{

public:

int vTo, timeFrom, timeTo;

Edge(int vTo, int timeFrom, int timeTo)

: vTo(vTo), timeFrom(timeFrom), timeTo(timeTo) {}

};

Qraf sinfini elan edək. O təpə nöqtələrinin n sayını ehtiva edir və g qonşuluq siyahısı ilə verilir.

class Graph

{

public:

int n;

vector<vector<Edge> > g;

Graph(int n = 1) : n(n)

{

g = vector<vector<Edge> >(n);

}

İstiqamətlənmiş tilin (From, To) əlavə edilməsi. Qatar From stansiyasından timeFrom zaman anında yola düşür və To stansiyasına timeTo zaman anında çatır.

void AddEdge(int From, int To, int timeFrom, int timeTo)

{

g[From].push_back(Edge(To,timeFrom,timeTo));

}

Dijkstra alqoritmi Source təpəsindən icra edilir. İkinci arqument kimi time massivi verilir: time[i] Source təpəsindən i təpəsinə çatmaq üçün ən qısa zamanı ehtiva edir.

void Dijkstra(int Source, vector<int> &time)

{

priority_queue<Prior, vector<Prior>, greater<Prior> > pq;

Növbəyə cütlüyü (0, Source) yerləşdirək, hesab edirik ki, time[Source] zamanı 0-a bərabərdir (Source təpəsindən onun özünə getmək 0 zamanda mümkündür).

pq.push(Prior(0,Source)); time[Source] = 0;

while(!pq.empty())

{

int v = pq.top().Vertex;

int d = pq.top().Time; pq.pop();

Növbənin başından cütlüyün (v, d) çıxarılmasının yalan olduğunu yoxlayırıq.

if (d > time[v]) continue;

v ilə qonşu olan to təpəsinə baxırıq. (v, to) tilinin qısaltmasını verməyə çalışırıq.

for(int i = 0; i < g[v].size(); i++)

{

time[v] v stansiyasına getmək üçün ən qısa zamanı ehtiva edir. Əgər (v, to) tili qatarın v stansiyasından to stansiyasına getmək üçün time[v] zamanından erkən çıxdığı haqqında informasiya ehtiva edərsə, onda biz bu qatara çatmırıq.

if (g[v][i].timeFrom < time[v]) continue;

Tilin getdiyi to tilini hesablayırıq.

int to = g[v][i].vTo ;

Əgər to stansiyasına (v, to) tili ilə time[to]-dakı zamandan erkən çatmaq mümkün olarsa, onda qısaltmanı veririk və cütlüyü (time[to], to) növbəyə yerləşdiririk.

if (time[to] > g[v][i].timeTo)

{

time[to] = g[v][i].timeTo;

pq.push(Prior(time[to],to));

}

}

}

}

};

Qraf göstəricisi təyin edək.

Graph *g;

Proqramın əsas hissəsi. Başlanğıc stansiyadan bütün stansiyalara gedilməsi mümkün olan ən qısa zamanları ehtiva edən time massivini verək.

scanf("%d %d %d",&n,&e,&m);

g = new Graph(n+1);

time = vector<int>(n+1,INF);

Giriş verilənlərini oxuyuruq. g qrafını qururuq.

for(i = 0; i < m; i++)

{

scanf("%d",&stations); PrevStation = -1;

for(j = 0; j < stations; j++)

{

scanf("%d %d",&CurStation,&CurTime);

Qatar PrevStation stansiyasından PrevTime zamanında çıxır, növbəti CurStation stansiyasına yola düşür və CurTime zaman anında stansiyaya çatır.

if (PrevStation != -1) g->AddEdge(PrevStation,CurStation,

PrevTime,CurTime);

PrevStation = CurStation; PrevTime = CurTime;

}

}

1 təpəsindən Dijkstra alqoritmini icra edirik.

g->Dijkstra(1,time);

Cavabı veririk.

if (time[e] == INF) printf("-1\n");

else printf("%d\n",time[e]);