776. Дороги
В Украине, как известно, существует множество проблем,
и одна из них — состояние дорог. Новый президент страны решил сосредоточиться
на развитии дорожной инфраструктуры. Его цель — построить дополнительные дороги
между городами так, чтобы из любого города можно было добраться до любого
другого (возможно, через промежуточные населённые пункты, не обязательно
напрямую). Разумеется, при этом необходимо построить как можно меньше новых
дорог.
Предположим, что все дороги в Украине являются
двусторонними (как уже существующие, так и те, которые предстоит построить), то
есть движение по ним возможно в обоих направлениях. При этом между двумя
городами может быть несколько дорог, а также могут существовать дороги, ведущие
из города в сам себя.
Вход. Первая строка содержит два
натуральных числа
n и m (1 ≤
n, m ≤ 10000) – количество городов и количество
уже существующих дорог. В следующих m строках записаны по два целых числа ai и bi (1 ≤ ai, bi ≤ n)
– номера городов, соединённых существующей дорогой.
Выход. Выведите минимальное количество дорог, которые
необходимо построить, чтобы из любого города можно было добраться до любого
другого.
|
Пример входа |
Пример выхода |
|
7 5 1 3 2 3 3 2 2 4 6 7 |
2 |
РЕШЕНИЕ
графы – поиск в глубину
Анализ алгоритма
Поскольку граф содержит 10000 вершин, для его хранения будем использовать
список смежности. На основе входного списка рёбер построим соответствующее
представление графа. Затем с помощью поиска в глубину определим количество
компонент связности. Число новых дорог, которые необходимо построить, будет
равно количеству компонент связности минус один.
Пример
Граф, приведённый в примере, имеет
следующий вид:
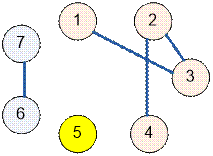
Граф состоит из трёх компонент
связности. Чтобы объединить их в одну, достаточно добавить два ребра.
Реализация алгоритма
Объявим список смежности g и массив used,
в котором будем отмечать посещённые вершины.
vector<vector<int> > g;
vector<int> used;
Функция dfs совершает поиск в глубину, начиная с вершины v.
void dfs(int v)
{
used[v] = 1;
for (int to : g[v])
if (!used[to]) dfs(to);
}
Основная часть
программы. Читаем входные данные.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
Читаем m ребер, строим список смежности графа.
for (i = 1; i <= m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Выполняем поиск в
глубину на несвязном графе. В переменной cnt подсчитываем количество
компонент связности.
used.resize(n
+ 1);
cnt
= 0;
for (i = 1; i <= n; i++)
if (used[i] == 0)
{
dfs(i);
cnt++;
}
Выводим количество
дорог, которые необходимо построить.
printf("%d\n", cnt - 1);
Реализация алгоритма –
система непересекающихся множеств
#include <stdio.h>
#define MAX 10001
int mas[MAX];
int Repr(int n)
{
while (n != mas[n]) n = mas[n];
return n;
}
void Union(int x, int y)
{
int x1 = Repr(x), y1 = Repr(y);
if (x1 == y1) return;
mas[x1] = y1;
}
int a, b, i, j, n, m, count;
int main(void)
{
scanf("%d
%d", &n, &m);
for (i = 1; i
<= n; i++) mas[i] = i;
for (i = 0; i <
m; i++)
{
scanf("%d
%d", &a, &b);
Union(a, b);
}
count = 0;
for (i = 1; i
<= n; i++)
if (mas[i] == i)
count++;
printf("%d\n", count - 1);
return 0;
}
Java реализация
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g;
static boolean used[];
static int n, m;
static void
dfs(int v)
{
used[v] = true;
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == false) dfs(to);
}
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
used = new boolean[n+1];
g = new ArrayList[n+1];
for(int i = 0; i <= n; i++)
g[i] = new
ArrayList<Integer>();
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
g[b].add(a);
}
int cnt = 0;
for(int i = 1; i <= n; i++)
if (used[i] == false)
{
dfs(i);
cnt++;
}
System.out.println(cnt - 1);
con.close();
}
}
Python реализация
import sys
sys.setrecursionlimit(1000000)
Функция dfs совершает поиск в глубину, начиная с вершины v.
def dfs(v):
used[v] = 1
for to in g[v]:
if not used[to]:
dfs(to)
Основная часть программы. Читаем входные данные.
n, m = map(int, input().split())
g = [[] for _ in range(n + 1)]
used = [0] * (n + 1)
Читаем m ребер, строим список смежности графа.
for _ in range(m):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Выполняем поиск в глубину на несвязном графе. В
переменной cnt подсчитываем количество компонент связности.
cnt = 0
for i in range(1, n + 1):
if not used[i]:
dfs(i)
cnt += 1
Выводим количество дорог, которые необходимо
построить.
print(cnt - 1)