776. Roads
As is well known, Ukraine faces numerous challenges, one of which is the
condition of its roads. The new president of the country has decided to focus
on developing the road infrastructure. His goal is to build additional roads
between cities so that it becomes possible to travel from any city to any other
(possibly through intermediate cities, not necessarily directly). Naturally,
the number of new roads must be as small as possible.
Assume that all roads in Ukraine are bidirectional (both existing ones
and those that will be built), meaning that travel is possible in both
directions. Furthermore, there may be multiple roads between a pair of cities,
and roads connecting a city to itself may also exist.
Input. The first line
contains two positive integers n and m (1 ≤ n, m ≤ 10000) – the number of cities and the number of existing roads. Each of the
following m lines contains two integers ai and bi (1 ≤ ai, bi ≤ n) – the numbers of the cities connected by an existing road.
Output. Print the minimum
number of roads that must be built so that it is possible to travel from any
city to any other.
|
Sample input |
Sample output |
|
7 5 1 3 2 3 3 2 2 4 6 7 |
2 |
SOLUTION
graphs – depth first search
Algorithm analysis
Since the graph contains 10,000
vertices, we’ll use an adjacency list to store it. Based on the input list of edges,
build the corresponding representation of the graph. Then, using depth-first
search, determine the number of connected components. The number of new roads
that need to be built is equal to the number of connected components minus one.
Example
The graph shown in the example has
the following structure:
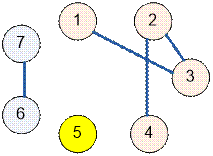
The graph consists of three connected
components. To merge them into one, it is enough to add two edges.
Algorithm implementation
Declare an
adjacency list g and an array used to mark the visited vertices.
vector<vector<int> > g;
vector<int> used;
The function dfs performs a depth-first search starting from vertex v.
void dfs(int v)
{
used[v] = 1;
for (int to : g[v])
if (!used[to]) dfs(to);
}
The main part of the program. Read the input data.
scanf("%d %d", &n, &m);
g.resize(n
+ 1);
Read m edges and build the adjacency list of the graph.
for (i = 1; i <= m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Perform a depth-first search on the
disconnected graph. The variable cnt is used to count the number of
connected components.
used.resize(n
+ 1);
cnt
= 0;
for (i = 1; i <= n; i++)
if (used[i] == 0)
{
dfs(i);
cnt++;
}
Print the number of roads that need to be built.
printf("%d\n", cnt - 1);
Algorithm implementation – disjoint sets
#include <stdio.h>
#define MAX 10001
int mas[MAX];
int Repr(int n)
{
while (n != mas[n]) n = mas[n];
return n;
}
void Union(int x, int y)
{
int x1 = Repr(x), y1 = Repr(y);
if (x1 == y1) return;
mas[x1] = y1;
}
int a, b, i, j, n, m, count;
int main(void)
{
scanf("%d
%d", &n, &m);
for (i = 1; i
<= n; i++) mas[i] = i;
for (i = 0; i <
m; i++)
{
scanf("%d
%d", &a, &b);
Union(a, b);
}
count = 0;
for (i = 1; i
<= n; i++)
if (mas[i] == i)
count++;
printf("%d\n", count - 1);
return 0;
}
Java implementation
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g;
static boolean used[];
static int n, m;
static void dfs(int v)
{
used[v] = true;
for(int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == false) dfs(to);
}
}
@SuppressWarnings("unchecked")
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
used = new boolean[n+1];
g = new
ArrayList[n+1];
for(int i = 0; i <= n; i++)
g[i] = new
ArrayList<Integer>();
for (int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
g[b].add(a);
}
int cnt = 0;
for(int i = 1; i <= n; i++)
if (used[i] == false)
{
dfs(i);
cnt++;
}
System.out.println(cnt - 1);
con.close();
}
}
Python implementation
Increase the recursion stack size.
import sys
sys.setrecursionlimit(1000000)
The function dfs performs a depth-first search starting from vertex v.
def dfs(v):
used[v] = 1
for to in g[v]:
if not used[to]:
dfs(to)
The main part of the program. Read the input data.
n, m = map(int, input().split())
g = [[] for _ in range(n + 1)]
used = [0] * (n + 1)
Read m edges and build the adjacency list of the graph.
for _ in range(m):
a, b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Perform a depth-first search on the
disconnected graph. The variable cnt is used to count the number of
connected components.
cnt = 0
for i in range(1, n + 1):
if not used[i]:
dfs(i)
cnt += 1
Print the number of roads that need to be built.
print(cnt - 1)