798. Platforms
In older games one can run into the next situation. The
hero jumps along the platforms that hang in the air. He must move himself from
one side of the screen to the other. When the hero jumps from one platform to
the neighboring, he spends |y2
– y1| energy, where y1 and y2 are the heights where these platforms hang. The hero
can make a super jump that allows him to skip one platform, but it takes him 3
* | y3 – y1| energy.
You are given the heights of the platforms in order
from the left side to the right. Find the minimum amount of energy to get from
the 1-st (start) platform to the n-th
(last). Print the list (sequence) of the platforms that the hero must pass.
Input. The first
line contains the number of platforms n
(2 ≤ n ≤ 100000). The second
line gives n integers – the heights
of the platforms, which absolute values are not grater than 400.
Output. Print
in the first line the minimum amount of energy to get from the 1-st platform to
the n-th. Print in the second line
the number of platforms to pass. Give in the third line the list of these
platforms.
|
Sample input 1 |
Sample output 1 |
|
4 1 2 3 30 |
29 4 1 2 3 4 |
|
|
|
|
Sample input 2 |
Sample output 2 |
64 6 15 5 10 12 |
1251 2 4 5 6 |
SOLUTION
dynamic
programming
Algorithm analysis
Let
e[i] contains the minimum amount of
energy sufficient to get from platform 1 to platform i. Obviously, e[1] = 0 (to get from the first platform to the first
is zero energy), and e[2] = |y2
– y1|, since the second
platform can only be reached from the first one.
In
cell p[i], we’ll store the number of
the platform from which we jumped to the i-th.
Initially, we set p[1] = -1 (initially we are on the first platform), and also
p[2] = 1.

To
the i-th platform (i ≥ 3) you can jump either from (i – 1) -th, spending e[i – 1] + |yi – yi-1|
energy, or from (i – 2)-th, having
made a super jump and spending e[i –
2] + 3·|yi – yi-2| energy. So
e[i] = min( e[i – 1] + |yi –
yi-1| , e[i – 2] + 3·|yi – yi-2|
)
If
to the i-th platform the jump is
performed from (i – 1) -th, then set
p[i] = i – 1. If from (i – 2)
-th, then we set p[i] = i – 2. To find the number of platforms
on which jumps from the first to the n-th
were performed, one should walk from the n-th
platform to the first one each time moving from the i-th platform to p[i]
-th.
Example
Consider
the second test case. 6 platforms with specified heights are as follows:
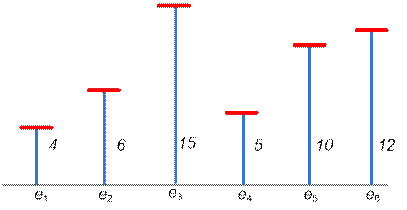
Calculate
the spent energy when jumping:
e[1]
= 0, p[1] = -1;
e[2]
= |6 – 4| = 2, p[2] = 1;
e[3]
= min(e[2] + |15 – 6|, e[1] + 3 * |15 – 4|) = min(11, 33) = 11, p[3] = 2;
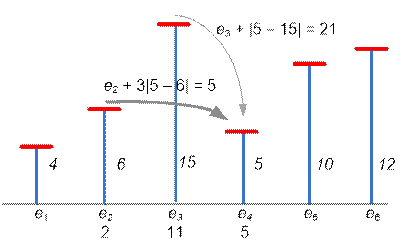
e[4]
= min(e[3] + |5 – 15|, e[2] + 3 * |5 – 6|) = min(21, 5) = 5, p[4] = 2;
e[5]
= min(e[4] + |10 – 5|, e[3] + 3 * |10 – 15|) = min(10, 26) = 10, p[5] = 4;
e[6]
= min(e[5] + |12 – 10|, e[4] + 3 * |12 – 5|) = min(12, 26) = 12, p[6] = 5;
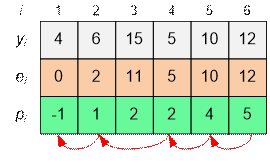
To
restore the path, move from the final (6-th) platform back along the indexes of
p[i]:

The
list of platforms to go through is as follows:
1,
2, 4, 5, 6
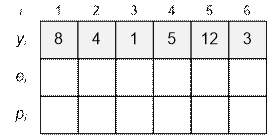
Exercise
Fill
the arrays with the next input data.
Algorithm realization
Declare
the necessary arrays.
#define MAX 100001
int y[MAX], e[MAX], p[MAX], res[MAX];
Read the input data.
scanf("%d",&n);
for(i = 1; i <= n; i++) scanf("%d",&y[i]);
Set the initial values of the cells.
e[1] = 0; e[2] = abs(y[2] - y[1]);
p[1] = -1; p[2] = 1;
In the loop calculate the values e[i] and p[i] (3 ≤ i ≤ n), comparing e[i – 1] +
|yi – yi-1| and e[i – 2] + 3*|yi
– yi-2|.
for(i = 3; i <= n; i++)
{
a = e[i-1] + abs(y[i] - y[i-1]);
b = e[i-2] + 3 * abs(y[i] - y[i-2]);
if (a < b)
{
e[i] = a; p[i] = i - 1;
} else
{
e[i] = b; p[i] = i - 2;
}
}
In the variable ptr
we calculate the number of platforms that need to be passed. At the same time
to the platform i we should jump from
the platform p[i].
ptr = 0;
for(i = n; i > 0; i = p[i])
res[ptr++] = i;
The minimum amount of energy that should be spent to
get from the first platform to the n-th
is equal to e[n]. The number of
platforms to go through is ptr.
printf("%d\n%d\n",e[n],ptr);
Print the list of platform numbers.
for(i = ptr - 1; i >= 0; i--)
printf("%d
",res[i]);
printf("\n");
Java realization
import java.util.*;
public class Main
{
public static int MAX = 100001;
static int y[] = new int[MAX];
static int e[] = new int[MAX];
static int p[] = new int[MAX];
static int res[] = new int[MAX];
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
for(int i = 1; i <= n; i++)
y[i] = con.nextInt();
e[1] = 0;
e[2] = Math.abs(y[2] - y[1]);
p[1] = -1; p[2] = 1;
for(int i = 3; i <= n; i++)
{
int a = e[i-1] + Math.abs(y[i] - y[i-1]);
int b = e[i-2] + 3 * Math.abs(y[i] - y[i-2]);
if (a < b)
{
e[i] = a; p[i] = i - 1;
} else
{
e[i] = b; p[i] = i - 2;
}
}
int ptr = 0;
for(int i = n; i > 0; i = p[i])
res[ptr++] = i;
System.out.println(e[n] + "\n" + ptr);
for(int i = ptr - 1; i >= 0; i--)
System.out.print(res[i] + " ");
System.out.println();
con.close();
}
}
Python realization
n = int(input())
y = [0] + list(map(int, input().split()))
e = [0] * (n + 1)
p = [0] * (n + 1)
e[1], e[2] = 0, abs(y[2] - y[1])
p[1], p[2] = -1, 1
for i in range(3, n+1):
a = e[i - 1] + abs(y[i] - y[i - 1]);
b = e[i - 2] + 3 * abs(y[i] - y[i - 2]);
if a < b: e[i], p[i] = a, i - 1;
else: e[i], p[i] = b, i - 2;
res = []i = nwhile i > 0:
res.append(i) i = p[i] print(e[-1])
print(len(res))
print(*res[::-1])