799. Buying tickets
There is a queue of n people
to buy tickets to a musical premiere. Each person wants to buy exactly one
ticket. Only one ticket-office was working, therefore ticketing was very
slowly, bringing “guests” to despair. The smartest people quickly noticed that,
as a rule, the cashier sells several tickets in one hand faster than when those
same tickets are sold one by one. So, they proposed for several people standing
in a row to give money to the first one of them, so that he would buy tickets
for all.
However, to deal with speculators, the cashier decided to sell maximum
of three tickets per person, so to agree with each other in such way can only
two or three successive persons.
It is known that to sell one ticket for the i-th person in the queue takes ai seconds,
to sell two tickets takes bi seconds, to sell three tickets takes ci seconds. Write a program that calculates the minimum time to serve all
the customers.
Please note that tickets for a group of united people always buys the first
one. Also, no one buys extra tickets for speeding up the process (i.e. the tickets that are not wanted).
Input. The first line
contains the number of people in the queue n (1 ≤ n ≤ 5000).
Then n triples of positive integers ai, bi, ci are given. Each of these numbers is not greater than 3600. People
in the queue are numbering starting from the booking office.
Output. Print the minimum time in seconds to serve all customers.
|
Sample input |
Sample output |
|
5 5 10 15 2 10 15 5 5 5 20 20 1 20 1 1 |
12 |
SOLUTION
dynamic
programming
Algorithm analysis
Let t[i] be the minimum time during which it is possible to serve customers from the
first to the i-th. Set t[0] = 0. If there is one customer, he can buy
himself a ticket in a1 seconds, therefore t[1] = a1. Two buyers will either
buy tickets for themselves in a1 + a2 seconds, or they will cooperate and
the first one will take two tickets in b1 seconds. Thus, t[2] = min (a1 + a2, b1). In the presence of three or more
buyers, all types of cooperation described in the problem statement are
possible, therefore, write the recurrence relation:
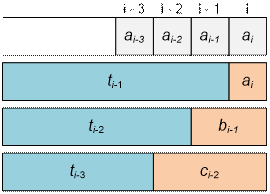
t[i]
= min(t[i – 1] + ai, t[i – 2] + bi-1, t[i
– 3] + ci-2)
If the i-th customer takes the ticket
himself, then at least the time t[i – 1] + ai is spent.
If the (i – 1)-th customer takes two tickets (for himself and for the i-th), then at least the time t[i
– 2] + bi-1 is spent.
If the (i – 2)-th customer takes three tickets (for himself, for the (i – 1)-th and for the i-th), then at least the time t[i – 3] + ci-2 is spent.
It remains to find the minimum among
the three expressions, which equals to the shortest time in which all i buyers can
purchase tickets.
Algorithm realization
Store
the values ai, bi, ci in arrays a, b, c.
#define MAX 5010
int a[MAX],
b[MAX], c[MAX], t[MAX];
Read the input data.
scanf("%d",&n);
for(i = 1; i <= n; i++) scanf("%d %d %d",&a[i],&b[i],&c[i]);
Initialize the base cases.
t[0] = 0; t[1] = a[1]; t[2] = min(a[1] + a[2],b[1]);
In the loop compute the values of t[i].
for(i = 3; i <= n; i++)
t[i] = min(t[i-1] +
a[i], t[i-2] + b[i-1], t[i-3] + c[i-2]);
Print the result. The minimum time it takes to serve customers from the first to
the n-th is t[n].
printf("%d\n",t[n]);
Java realization
import
java.util.*;
public class Main
{
public static int MAX = 5010;
static int a[] = new int[MAX];
static int b[] = new int[MAX];
static int c[] = new int[MAX];
static int t[] = new int[MAX];
public static int min(int a, int b, int c)
{
return Math.min(Math.min(a,b),c);
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int n = con.nextInt();
for(int i = 1; i <= n; i++)
{
a[i] = con.nextInt();
b[i] = con.nextInt();
c[i] = con.nextInt();
}
t[0] = 0; t[1] = a[1]; t[2] = Math.min(a[1] + a[2],b[1]);
for(int i = 3; i <= n; i++)
t[i] = min(t[i-1] + a[i], t[i-2] + b[i-1], t[i-3] + c[i-2]);
System.out.println(t[n]);
con.close();
}
}
Python realization
n = int(input())
a = [0] * 5001
b = [0] * 5001
c = [0] * 5001
for i in range(1,n+1):
a[i], b[i], c[i] = map(int, input().split())
t = [0] * (n+1)
t[0] = 0;
t[1] = a[1];
if n > 1 : t[2] = min(a[1] + a[2], b[1]);
for i in range(3, n+1):
t[i] = min(t[i-1] + a[i], t[i-2] + b[i-1], t[i-3] + c[i-2])
print(t[-1])