7945. Карлики

 

Давным-давно возникла большая дискуссия между гномами в Гномляндии. Правительство хотело ввести удостоверение личности для всех жителей.

Большинство гномов соглашаются быть маленькими, но они не хотят быть измеренными. Поэтому правительство позволило им заменить поле “высота гнома” в своем удостоверении личности полем “относительная высота гнома”. Для изготовления удостоверений личности гномы брали интервью об их относительных размерах. По какой-то причине правительство подозревает, что по крайней мере один из опрошенных гномов возможно солгал.

Можете ли Вы помочь узнать, предполагает ли предоставленная информация существование хотя бы одного карлика сказавшего неправду?

 

Вход. Состоит из:

·        первая строка содержит количество утверждений n (1 ≤ n ≤ 105);

·        следующие n строк описывают отношения между карликами. Каждое отношение задается строкой вида “s1 < s2” или “s1 > s2”, утверждающей что карлик s1 меньше или выше карлика s2. s1 и s2 – различные имена карликов.

Имя карлика состоит из не более 20 букв от “A” до “Z” и “a” до “z”. Имя карлика не содержит пробелов. Количество карликов не превосходит 104.

 

Выход. Выведите “impossible” если утверждения не совместимы, иначе выведите “possible”.

 

Пример входа 1

Пример выхода 1

3

Dori > Balin

Balin > Kili

Dori < Kili

impossible

 

 

Пример входа 2

Пример выхода 2

3

Dori > Balin

Balin > Kili

Dori > Kili

possible

 

 

РЕШЕНИЕ

графы - циклы

 

Анализ алгоритма

Построим ориентированный граф, вершинами которого будут имена карликов. Для этого каждому имени поставим в соответствие некоторое целое число. Для отношения s1 < s2 проведем ориентированное ребро из s1 в s2.

Набор заданных утверждений будет не совместимым, если построенный граф будет иметь циклы. Ориентированный граф содержит цикл, если при поиске в глубину существует ребро, ведущее в серую вершину.

 

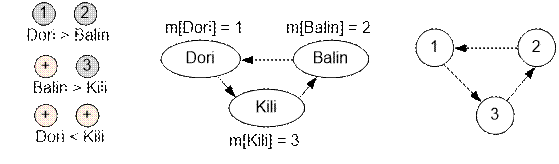
Пример

Приведенные в примерах графы имеют вид:

Первый граф содержит цикл, поэтому заданные отношения между карликами невозможны.

Рассмотрим построение графа для первого теста. Первым имеем встречается Dori. Установим m[Dori] = 1. Следующим встречается имя Balin. Установим m[Balin] = 2. Во втором условии первым встечаетя Balin. Однако m[Balin] не равен 0 (ему уже присвоено число). Следующим идет Kili. Установим m[Kili] = 3.

 

Реализация алгоритма

Ориентировнный граф храним в списке смежности g. Объявим массив used использованных вершин при обходе в глубину. Соответствие между именами гномов и номерами вершин храним в отображении m (гному с именем s соответствует вершина номер m[s]).

 

vector<vector<int> > g;

vector<int> used;

map<string,int> m;

 

Функция dfs реализует поиск в глубину из вершины v.

 

void dfs(int v)

{

  if (flag == 1) return;

  used[v] = 1;

  for(int i = 0; i < g[v].size(); i++)

  {

    int to = g[v][i];

 

Ребро (v, to) является текущим рассматриваемым. Если оно ведет в серую вершину, то найден цикл, устанавливаем flag = 1.

 

    if (used[to] == 1)

    {

      flag = 1;

      return;

    }

    if (used[to] == 0) dfs(to);

  }

 

Вершина v по завершению обработки становится черной.

 

  used[v] = 2;

}

 

Основная часть программы. Читаем количество отношений stat между карликами. Поскольку количество карликов не превосходит 104, то количество вершин в графе не более 10000.

 

scanf("%d",&stat);

g.resize(10001); used.resize(10001,0);

 

В переменной n подсчитываем количество карликов.

 

n = 0;

 

Обрабатываем stat утверждений. Для каждого утверждения строим ориентированное ребро.

 

for(i = 0; i < stat; i++)

{

 

Читаем отношение s1 < s2 или s1 > s2.

 

  scanf("%s %c %s",s1,&ch,s2);

 

Значение m[s] содержит номер вершины для карлика s. Если m[s] еще не установлено (m[s] = 0), то присваиваем номер вершины ++n карлику  с именем s.

 

  if (m[s1] == 0) m[s1] = ++n;

  if (m[s2] == 0) m[s2] = ++n;

 

Отношение s1 < s2 для карлиов означает существование ориентированного ребра от m[s1] к m[s2].

 

  int from = m[s1], to = m[s2];

  if (ch == '<')

    g[from].push_back(to);

  else

    g[to].push_back(from);

}

 

Запускам поиск в глубину на ориентированном графе. flag = 0 означает что в графе нет циклов.

 

flag = 0;

for(i = 1; i <= n; i++)

{

  if (!used[i]) dfs(i);

  if (flag == 1) break;

}

 

В зависимости от значения переменной flag выводм ответ.

 

if (flag == 1) printf("impossible\n"); else printf("possible\n");

 

Java реализация

 

import java.util.*;

 

public class Main

{

  static ArrayList<Integer>[] g;

  static HashMap<String, Integer> map = new HashMap<>(); 

  static int used[];

  static int n, flag;

 

  static void dfs(int v)

  {

    if (flag == 1) return;

    used[v] = 1;

    for(int i = 0; i < g[v].size(); i++)

    {

      int to = g[v].get(i);

      if (used[to] == 1)

      {

        flag = 1;

        return;

      }

      if (used[to] == 0) dfs(to);

    }

    used[v] = 2;

  }

 

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);

    int stat = con.nextInt();

    g = new ArrayList[10001];

    for (int i = 0; i < 10001; i++)

      g[i] = new ArrayList<Integer>();

   

    n = 0;   

    for(int i = 0; i < stat; i++)

    {

      String s1 = con.next();

      char ch = con.next().charAt(0);

      String s2 = con.next();

      if (!map.containsKey(s1)) map.put(s1, ++n);

      if (!map.containsKey(s2)) map.put(s2, ++n);

     

      Integer from = map.get(s1), to = map.get(s2);

      if (ch == '<')

        g[from].add(to);

      else

        g[to].add(from);

    }

   

    used = new int[n+1];

    flag = 0;

    for(int i = 1; i <= n; i++)

    {

      if (used[i] == 0) dfs(i);

      if (flag == 1) break;

    }

 

    if (flag == 1) System.out.println("impossible");

    else System.out.println("possible");

  }

}