7945. Gnomes
Long ago, a fierce debate broke out in Gnomeland. The government planned
to introduce identity cards for all residents.
Most gnomes agreed that they are small, but they were strongly opposed
to being measured. In response to their protests, the government allowed them
to replace the “gnome height” field in the identity card with a field called
“relative gnome height.” To issue these identity cards, gnomes were interviewed
and asked to express their relative height compared to others. However, for
some reason, the government suspects that at least one of the gnomes may have lied.
Can you determine whether the provided information allows for the
possibility that at least one gnome is not telling the truth?
Input. The first line contains the number of
statements n (1 ≤ n ≤ 105).
Each of the following n lines describes a relationship
between two gnomes. Each statement is given in the form “s1 < s2” or “s1 > s2”,
indicating that gnome s1 is
shorter or taller than gnome s2,
respectively. Here, s1 and s2 are distinct gnome names.
A gnome’s name consists of no more than 20 Latin letters
(uppercase “A” – “Z” and lowercase “a” – “z”). Gnome names do not contain
spaces. The total number of distinct gnomes does not exceed 104.
Output. Print “impossible” if the statements contradict each other, otherwise
print “possible”.
|
Sample input 1 |
Sample output 1 |
|
3 Dori > Balin Balin > Kili Dori < Kili |
Impossible |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
3 Dori > Balin Balin > Kili Dori > Kili |
Possible |
SOLUTION
graphs
- cycles
Algorithm analysis
Construct a directed graph in which the vertices
correspond to the names of the dwarves. To do this, assign a unique integer to
each name. If a statement says that dwarf s1
is shorter than dwarf s2
(i.e., s1 < s2), add a directed edge from
vertex s1 to vertex s2.
![]()
A set of
statements is considered inconsistent if the constructed graph contains cycles.
A directed graph contains a cycle if, during depth-first search, an edge leads
to a vertex that is already in the process of being explored – a so-called “gray” vertex.
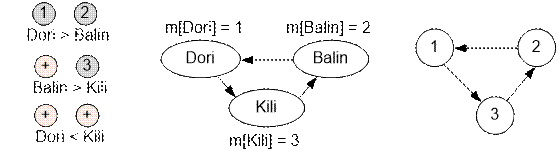
Example
The graphs
corresponding to the examples given in the problem statement are as follows:

The first
graph contains a cycle, so the specified relationships between the dwarves are
contradictory and cannot all be true at the same time.
Let’s
examine the construction of the graph for the first test case. The first name
encountered is Dori. Assign it a
number: m[Dori] = 1. Next comes Balin, so set m[Balin] = 2. In the second
statement, Balin comes first. However, since it has already been assigned a
value, leave it unchanged. The next name is Kili, assign m[Kili] = 3.
Algorithm implementation
The directed graph is stored as an adjacency list g.
For depth-first search, use an array used that marks the state of the
vertices. The mapping between dwarf names and vertex numbers is stored in the
dictionary name_to_id – the dwarf
with name s corresponds to the vertex with number name_to_id[s].
vector<vector<int>
> g;
vector<int> used;
unordered_map<string, int> name_to_id;
The function get_id assigns a unique integer
identifier to a dwarf’s name. Identifiers are numbered from 0 up to (but not
including) id.
int get_id(string name)
{
If a dwarf with the name name has already been
encountered, the function returns the corresponding identifier.
if (name_to_id.count(name)) return name_to_id[name];
Otherwise, the dwarf with the name name is
assigned the current identifier id, after which the value of id is
incremented by 1.
return name_to_id[name] = id++;
}
The function dfs implements a depth-first search starting from the
vertex v.
void dfs(int v)
{
used[v] = 1;
for (int to : g[v])
{
The edge (v, to) is the currently considered edge. If
it leads to a gray vertex, it means a cycle has been
detected, and the variable flag is set to 1.
if (used[to] == 1)
{
flag = 1;
return;
}
If the vertex v is not visited, continue the depth-first search from it.
if (used[to] == 0) dfs(to);
}
After processing all the children, the vertex v
becomes black.
used[v] = 2;
}
The main
part of the program reads the number of statements n about the
relationships between dwarfs. Since the total number of distinct dwarfs does
not exceed 104, the
number of vertices in the graph also does not exceed 104.
cin >> n;
g.resize(10001); used.resize(10001,0);
The numbering of dwarfs starts from 0.
id = 0;
Process n
statements. For each statement, construct a directed edge in the graph.
for (i = 0; i < n; i++)
{
Read a
relation of the form s1
< s2 or s1 > s2.
cin >> l >> op >> r;
Assign a unique numeric identifier to each dwarf’s name – the vertex number in the
graph.
u = get_id(l);
v = get_id(r);
Construct a directed edge of the graph.
if (op == "<")
g[u].push_back(v);
else
g[v].push_back(u);
}
flag = 0 means
that the graph contains no cycles.
flag = 0;
Run a
depth-first search on the directed graph. The graph’s vertices are numbered from 0 to id – 1.
for (i = 0; i < id; i++)
{
if (!used[i]) dfs(i);
if (flag == 1) break;
}
Depending on the value of the variable flag, print the answer.
if (flag == 1) printf("impossible\n");
else printf("possible\n");
Java implementation
import java.util.*;
public class Main {
static List<List<Integer>> g = new ArrayList<>();
static int[] used;
static Map<String, Integer> nameToId = new HashMap<>();
static int id = 0;
static boolean hasCycle = false;
static int getId(String name) {
if (!nameToId.containsKey(name))
nameToId.put(name, id++);
return nameToId.get(name);
}
static void dfs(int v) {
used[v] = 1;
for (int to : g.get(v)) {
if (used[to] == 1) {
hasCycle = true;
return;
}
if (used[to] == 0) dfs(to);
}
used[v] = 2;
}
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
used = new int[10001];
for (int i = 0; i < 10001; i++)
g.add(new ArrayList<>());
for (int i = 0; i < n; i++) {
String l = sc.next();
String op = sc.next();
String r = sc.next();
int u = getId(l);
int v = getId(r);
if (op.equals("<"))
g.get(u).add(v);
else
g.get(v).add(u);
}
for (int i = 0; i < id; i++) {
if (used[i] == 0) {
dfs(i);
if (hasCycle) break;
}
}
System.out.println(hasCycle ? "impossible" : "possible");
}
}