8508. Числа
Юный
Андрей любит играть с числами. Сначала он записал целое число a. Затем он записывает некоторый
делитель d1 числа a (1 < d1 < a),
стирает a и записывает вместо него a1 = a + d1. Далее
он выбирает некоторый делитель d2
числа a1 (1 < d2 < a1), стирает a1
и записывает вместо него a2
= a1 + d2.
То есть на
каждом шаге выбирается некоторый целочисленный делитель текущего числа, но не 1
и не само число, и на него увеличивается текущее число.
Можно ли
записать число b, если начать с a?
Вход. В одной
строке находятся два целых числа a и b (2 ≤ a < b ≤ 1012).
Выход. Если
решения не существует, вывести "Impossible" (без кавычек). Если
решение существует, следует вывести последовательность чисел, начиная с a и заканчивая b, каждое число следует выводить в отдельной строке. Вам не следует
выводить кратчайшую последовательность, однако требуется найти такую, которая
содержит не более 500 чисел. Гарантируется, что если существует решение для
заданных a и b, то и существует последовательность из не более чем 500 чисел.
|
Пример входа 1 |
Пример выхода 1 |
|
12 57 |
12 18 24 36 48 54 57 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
3 6 |
Impossible |
РЕШЕНИЕ
математика
Анализ алгоритма
Если a простое, то ответ Impossible, так как
число a не имеет делителей кроме 1 и
самого себя, а их прибавлять нельзя согласно условию задачи.
Пусть
существует искомая последовательность, и число b было получено непосредственно из c. То есть некоторый делитель d
числа c был прибавлен к c и получилось b. Поскольку d – делитель
числа c, то c = d * k для некоторого k. Запишем это равенство: c
+ d = b или d * k + d = b,
или d * (k + 1) = b, откуда
следует что b составное. Таким
образом если b простое, то ответ
Impossible.
Искомую
последовательность чисел будем строить во множестве st. Занесем a и b
во множество st.
Рассмотрим,
что делать когда a и b составные. Если a нечетно, то добавим к a
любой его нечетный делитель d,
получив четное число: a = a + d.
Если b нечетно, то вычтем из b любой его нечетный делитель d, получив четное число: b = b
– d. Занесем новые значения a и b
во множество st.
Теперь
осталось из a получить b, где a и b четные. Для этого
будем прибавлять каждый раз к текущему числу a наибольшую степень двойки p
(a = a + p), удовлетворяющую
следующим условиям:
·
p является
делителем a;
·
p является
наибольшей степенью двойки;
·
p не равно
1 и не равно a;
·
p ≤ b – a,
это условие необходимо чтобы мы не перешагнули через b;
При помощи
такого алгоритма всегда из a можно
получить b.
Пример
Пусть a = 12, b = 57. Оба числа составные. Инициализируем множество st = {12,
57}. Число a четное, оставляем его.
Число b нечетное, вычтем из него
наименьший делитель, отличный от 1. Таким делителем будет d = 3, пересчитаем: b =
57 – 3 = 54. Занесем новые числа a и b во множество: st = {12, 54, 57}.
Теперь a = 12, b = 54. Пока a < b на
каждой итерации прибавляем к a
максимальную степень двойки, являющуюся его делителем.
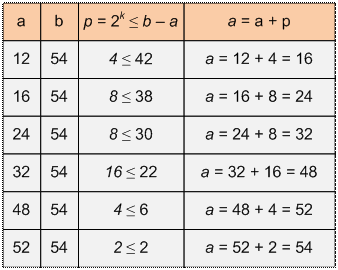
Указанная
последовательность отличается от приведенной в примере. Существует не
единственное решение.
Реализация алгоритма
Проверка
числа n на простоту.
int IsPrime(long
long n)
{
for(long long i = 2; i * i <= n; i++)
if(n % i == 0) return
0;
return 1;
}
Читаем
входные числа a и b.
scanf("%lld %lld",&a,&b);
Если одно из чисел a
или b простое, то ответ Impossible.
if(IsPrime(a) || IsPrime(b))
{
puts("Impossible");
return 0;
}
Заносим входные числа a и b во множество.
st.insert(a); st.insert(b);
Если a
нечетное, то прибавим к нему нечетный делитель, получим четное число.
if(a % 2 == 1)
for(i = 2; i * i <= a; i++)
if(a % i == 0)
{
a = a + i;
break;
}
Если b
нечетное, то вычтем из него нечетный делитель, получим четное число.
if(b % 2 == 1)
for(i = 2; i * i <= b; i++)
if(b % i == 0)
{
b = b - i;
break;
}
Теперь числа a
и b четные, разность между ними
четная. Заносим числа во множество. Если a
> b, то ответ Impossible.
st.insert(a); st.insert(b);
if(b < a)
{
puts("Impossible");
return 0;
}
Заносим число а
во множество. Прибавляем к а
максимальную степень двойки p,
являющуюся его делителем, и не равную значению а.
while(a < b)
{
st.insert(a);
p = 2;
while(a % (2 * p) == 0 && 2 * p <= b - a
&& 2 * p < a)
p = p * 2;
a += p;
}
Выводим искомую последовательность.
for(iter = st.begin(); iter !=
st.end(); iter++)
printf("%lld\n",*iter);