8594. Between A and B
Given nonnegative integers a and
b (a ≤ b) and
positive integer x. How many numbers
are there between a and b inclusively, divisible by x?
Input. Three numbers a, b and x (0 ≤ a
≤ b ≤ 1018, 1
≤ x ≤ 1018).
Output. Print the answer to the problem.
|
Sample input |
Sample output |
|
5 10 3 |
2 |
SOLUTION
mathematics
Algorithm analysis
Let f(n) be the amount of numbers on the segment [0; n] divisible by x. Let f(a, b)
be the amount of
numbers on the segment [a; b] divisible by x. Then the number of required numbers on the segment [a; b] equals to the amount of
numbers on segment [0; b] minus the amount of numbers on segment [0; a – 1]. So
f(a, b)
= f(b) – f(a – 1)
The amount of numbers from 0 to n, inclusive, divisible by x is n / x + 1. So
f(n) = n / x + 1
If
initially a = 0, then the answer will
be one term f(0, b), since the value f(0, a – 1)
does not make sense.
Example
In the sample given, we must find the value
f(5, 10) =
f(10) – f(4)
Let's find
the amount of
numbers from 0 to 10 inclusive, divisible by 3. These will be the numbers 0, 3,
6 and 9. Their amount equals to f(10) = 10
/ 3 + 1 = 4.
Let's find
the amount of
numbers from 0 to 4
inclusive, divisible by 3. These will be the numbers 0 and 3. Their amount equals to f(4) = 4 /
3 + 1 = 2.
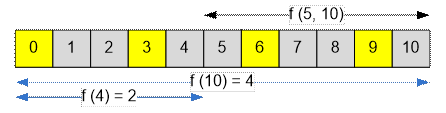
Therefore
f(5, 10) =
f(10) – f(4) = 4 – 2 = 2
Algorithm
realization
Read the input data.
scanf("%lld %lld %lld",&a,&b,&x);
Compute k = f(b), l
= f(a – 1).
k = b / x + 1;
l = (a - 1) / x + 1;
For a = 0 the answer
is k = f(b).
For a ≠ 0 the
answer is f(a, b) = f(b) – f(a – 1) = k – l.
if (a == 0) res = k; else
res = k - l;
Print the answer.
printf("%lld\n",res);
Java realization
import java.util.*;
public class Main
{
public static long a, b, x;
public static long f(long n)
{
if (n < 0) return 0;
return n / x + 1;
}
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
a = con.nextLong();
b = con.nextLong();
x = con.nextLong();
System.out.println(f(b) - f(a-1));
con.close();
}
}
Python realization
a, b, x = map(int,input().split())
def f(n):
if n < 0: return 0
return n // x + 1
print(f(b) - f(a - 1))