8596. Путешествие с
запада на восток
Есть n городов,
стоящих на прямой с запада на восток. Города пронумерованы от 1 до n, в порядке с запада на восток. Каждая
точка на прямой имеет свою одномерную координату, и точка ближе к востоку имеет
большую координату. Координата i-го
города – xi.
Сейчас Вы находитесь в 1 городе, и хотите
посетить все города. У вас есть два способа путешествовать:
·
Ходить по прямой.
При этом ваш уровень усталости будет увеличиваться на a единиц каждый раз, когда Вы будете перемещаться на
расстояние 1, независимо от направления.
·
Телепортироваться
в любую точку, которую хотите. Ваш уровень усталости будет увеличиваться на b единиц, независимо от
телепортированного расстояния.
Вход. Первая строка содержит три числа n (2 ≤ n ≤ 105), a и b (1 ≤ a, b ≤ 109).
Следующая строка содержит n целых
чисел x1, x2, ..., xn (1 ≤ xi ≤
109). Для всех i (1 ≤ i ≤ n – 1) имеет место неравенство xi < xi+1.
Выход. Выведите минимально возможный уровень усталости, при
котором вы посетите все города.
|
Пример входа 1 |
Пример выхода 1 |
|
4 2 5 1 2 5 7 |
11 |
|
|
|
|
Пример входа 2 |
Пример выхода 2 |
|
7 1 100 40 43 45
105 108 115 124 |
84 |
|
|
|
|
Пример входа 3 |
Пример выхода 3 |
|
7 1 2 24 35 40 68
72 99 103 |
12 |
РЕШЕНИЕ
динамическое
программирование
Анализ алгоритма
Рассмотрим
некоторый оптимальный (с минимальным
уровнем усталости) маршрут посещения всех городов. Его всегда можно
перестроить так, чтобы движение осуществлялось слева направо с последовательным
посещением городов. Например следующий маршрут

можно
переделать в

с тем же
уровнем усталости.
Пусть dp[i] – минимальный уровень усталости, с которым можно достичь
из города 1 город i двигаясь
последовательно по городам слева направо. Очевидно что dp[0] = 0.
В i-ый город
из (i – 1)-го можно попасть двумя путями:
·
идти по прямой.
Тогда усталость увеличится на a * (x[i] – x[i – 1]);
·
телепортироваться.
Тогда усталость увеличится на b;
Поскольку
общую усталось следует минимизировать, то необходимо выбрать тот путь, для
которого усталость меньшая. Таким образом
dp[i] = dp[i – 1] + min( a * (x[i] –
x[i – 1]), b)

Пример
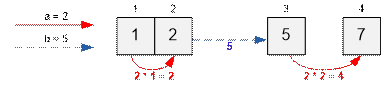
Тест 1. Из 1 города идем во 2-ой, после
телепортируемся в 3-ий. В конце идем в 4-ый. Уровень усталости в конце
будет
равен 2 * 1 + 5 + 2 * 2 = 11,
что является минимально возможным.
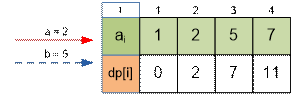
dp[1] = 0;
dp[2] = dp[1] + min( a * (2 – 1), b) = 0 + min( 2 * (2 – 1), 5) = 0 + 2
= 2;
dp[3] = dp[2] + min( a * (5 – 2), b) = 2 + min( 2 * (5 – 2), 5) = 2 + 5 = 7;
dp[4] = dp[3] + min( a * (7 – 5), b) = 7 + min( 2 * (7 – 5), 5) = 7 + 4 = 11;
Тест 2. Из города 1 просто идем во все города
вплоть до 7-го. В итоге уровень усталости будет равен 84, что
является минимально возможным.
Тест 3. Посещайте все города, в любом порядке, телепортируясь шесть раз. Уровень усталости будет
равен 12, что является минимально возможным.
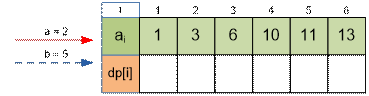
Упражнение
Вычислите значения dp[i] для следующих входных данных:
Реализация алгоритма
Читаем входные данные.
scanf("%d %d %d", &n, &a, &b);
res
= 0;
for (i = 0; i < n; i++)
scanf("%lld", &x[i]);
Вычисляем минимально
возможный уровень усталости при посещении всех городов.
for (i = 1; i < n; i++)
res = res + min(a*(x[i] - x[i - 1]), b);
Выводим ответ.
printf("%lld\n", res);
Реализация алгоритма – dp массив
#include <stdio.h>
#define MAX 100001
int i, n, a, b;
long long x[MAX], dp[MAX];
long long min(long long a, long long b)
{
return (a < b) ? a : b;
}
int main(void)
{
scanf("%d %d
%d", &n, &a, &b);
for (i = 1; i
<= n; i++)
scanf("%lld", &x[i]);
dp[1] = 0;
for (i = 2; i
<= n; i++)
dp[i] = dp[i - 1] +
min(a*(x[i] - x[i - 1]), b);
printf("%lld\n", dp[n]);
return 0;
}
Java реализация
import java.util.*;
class Main
{
static long x[] = new long[100001];
static long dp[] = new long[100001];
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int a = con.nextInt();
int b = con.nextInt();
for (int i = 1; i <= n; i++)
x[i] = con.nextInt();
dp[1] = 0;
for (int i = 2; i <= n; i++)
dp[i] = dp[i-1] + Math.min(a*(x[i] - x[i - 1]), b);
System.out.println(dp[n]);
con.close();
}
}