8596. Journey from west to east
There are n cities standing on a
straight line from west to east. The cities are numbered from 1 to n, in order from west to
east. Each point on the line has its own one-dimensional coordinate, and the
point closer to the east has a large coordinate. The coordinate of the i-th city is xi.
You are now in city 1,
and want to visit all cities. You have two ways to travel:
·
Walk in a straight line. At the same time, your
level of fatigue will increase by a units
each time you move a distance of 1, regardless of the
direction.
·
Teleport to any point you want. Your fatigue level
will increase by b units,
regardless of teleported distance.
Input. First line contains three
numbers n (2 ≤ n ≤ 105), a and b (1 ≤ a, b ≤ 109). Next line contains n integers x1, x2,
..., xn (1 ≤ xi ≤ 109). For all i (1 ≤ i ≤ n – 1) holds inequality xi < xi+1.
Output. Print the lowest possible
level of fatigue, at which you will visit all the cities.
|
Sample input 1 |
Sample output 1 |
|
4 2 5 1 2 5 7 |
11 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
7 1 100 40 43 45
105 108 115 124 |
84 |
|
|
|
|
Sample input 3 |
Sample output 3 |
|
7 1 2 24 35 40 68
72 99 103 |
12 |
SOLUTION
dynamic
programming
Algorithm
analysis
Consider
some optimal (with a minimum level of fatigue) route to visit all cities. It
can always be rebuilt so that the movement is carried out from left to right
with visits to consecutive cities.
For example the following route

can
be converted to

with
the same level of fatigue.
Let dp[i] be the the minimum level of fatigue with which you can reach city
i from city 1 moving sequentially
through cities from left to right. It is obvious that dp[0] = 0.
You
can get to the i-th city from the (i – 1) -th in two ways:
· walk in a straight line. Then fatigue level will increase by a * (x[i] – x[i – 1]);
· teleport. Then fatigue level will increase by b;
Since
overall fatigue should be minimized, it is necessary to choose the path for
which the fatigue is minimum. In this
way
dp[i] =
dp[i –
1] + min(
a * (x[i] – x[i – 1]),
b)

Example
Test 1. From
the 1st city we go to the 2nd, after we teleport to the 3rd. At the end we go
to the 4th. The fatigue level at the end will be 2 * 1 + 5 + 2 * 2 = 11, which
is the lowest possible.
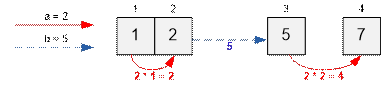
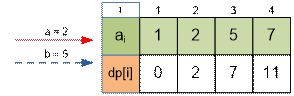
dp[1] = 0;
dp[2] = dp[1] + min( a * (2 – 1), b) = 0 + min( 2 * (2 – 1), 5) = 0 + 2 = 2;
dp[3] = dp[2] + min( a * (5 – 2), b) = 2 + min( 2 * (5 – 2), 5) = 2 + 5 = 7;
dp[4] = dp[3] + min( a * (7 – 5), b) = 7 + min( 2 * (7 – 5), 5) = 7 + 4 = 11;
Test 2. From
city 1 we just go to all cities up to 7th. As a result, the fatigue level will
be 84, which is the lowest possible.
Test 3. Visit
all cities, in any order, teleporting six times. The fatigue level will be 12,
which is the lowest possible.
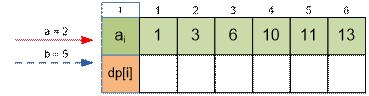
Exercise
Find the
values of dp[i] for the next input data:
Algorithm realization
Read the input data.
scanf("%d %d %d", &n, &a, &b);
res = 0;
for (i = 0; i < n; i++)
scanf("%lld", &x[i]);
Calculate the minimum possible level of fatigue
to visit all cities.
for (i = 1; i < n; i++)
res = res + min(a*(x[i] - x[i - 1]), b);
Print
the answer.
printf("%lld\n", res);
Algorithm realization – dp array
#include <stdio.h>
#define MAX 100001
int i, n, a, b;
long long x[MAX], dp[MAX];
long long min(long long a, long long b)
{
return (a < b) ? a : b;
}
int main(void)
{
scanf("%d %d %d", &n,
&a, &b);
for (i = 1; i <= n; i++)
scanf("%lld", &x[i]);
dp[1] = 0;
for (i = 2; i <= n; i++)
dp[i] = dp[i - 1] + min(a*(x[i] - x[i - 1]),
b);
printf("%lld\n", dp[n]);
return 0;
}
Java realization
import java.util.*;
class Main
{
static long x[] = new long[100001];
static long dp[] = new long[100001];
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int a = con.nextInt();
int b = con.nextInt();
for (int i = 1; i <= n; i++)
x[i] = con.nextInt();
dp[1] = 0;
for (int i = 2; i <= n; i++)
dp[i] = dp[i-1] + Math.min(a*(x[i] - x[i - 1]), b);
System.out.println(dp[n]);
con.close();
}
}