8636. Сортировка от 0 до n – 1

Задана последовательность чисел a₀, a₁, ... a_n-1, состоящая из n уникальных элементов, каждый из которых принадлежит промежутку [0; n – 1]. Обменом будем называть операцию (i, j) (0 ≤ i, j ≤ n – 1), которая меняет местами значения a_i и a_j. Отсортируйте последовательность, используя минимальное количество обменов. Выведите все произведенные обмены.

Вход. Первая строка содержит натуральное число n (n ≤ 10⁶). Вторая строка содержит n различных чисел из промежутка [0; n – 1].

Выход. В первой строке выведите минимальное количество проведенных обменов k. В следующих k строках выведите все произведенные обмены в виде пар (i, j).

Пример входа 1	Пример выхода 1
3 0 2 1	1 1 2
Пример входа 2	Пример выхода 2
5 4 0 3 2 1	3 1 4 3 2 4 0

РЕШЕНИЕ

сортировка - перестановки

Анализ алгоритма

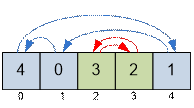
Представим перестановку в виде объединения циклов. Числа внутри одного цикла длины k можно отсортировать за k – 1 обмен. Например, перестановка (4 0 3 2 1) распадается на 2 цикла: (4 1 0) и (3 2). Следовательно, перестановку (4 0 3 2 1) можно отсортировать за 2 + 1 = 3 обмена.

Отсортированная перестановка всегда имеет вид (0, 1, 2, …., n – 1), то есть для каждого i должно выполняться равенство a_i = i. Переберем все возможные значения i и, если для некоторого i выполняется условие a_i ≠ i, отсортируем цикл, которому принадлежит элемент a_i, с помощью обменов.

Реализация алгоритма

Входную перестановку храним в массиве а.

vector<int> a;

vector<pair<int, int> > ans;

Читаем входную перестановку.

scanf("%d", &n);

a.resize(n);

for (i = 0; i < n; i++)

scanf("%d", &a[i]);

Если a_i ≠ i, то сортируем числа в цикле, которому принадлежит число a_i. Количество обменов подсчитываем в переменной cnt.

for (i = 0; i < n; i++)

while (a[i] != i)

{

ans.push_back(make_pair(i, a[i]));

swap(a[i], a[a[i]]);

cnt++;

}

Выводим количество обменов cnt и сами обмены.

printf("%d\n", cnt);

for (i = 0; i < ans.size(); i++)

printf("%d %d\n", ans[i].first, ans[i].second);