8636. Sort from 0 to n – 1
Given sequence
a0, a1, ... an-1 of n unique integers, each belongs to the
interval [0; n – 1].
The exchange is an operation (i, j)
(0 ≤ i, j ≤ n – 1) that swaps the values ai and aj. Sort the sequence using
the minimum number of exchanges. Print all exchanges.
Input. The first line contains
number n (n ≤ 106). Second line contains n
different
integers from the interval [0; n – 1].
Output. In the first line print the
minimum number of exchanges k. In the next k
lines print all
performed exchanges as pairs (i, j).
|
Sample input 1 |
Sample output 1 |
|
3 0 2 1 |
1 1 2 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
5 4 0 3 2 1 |
3 1 4 3 2 4 0 |
SOLUTION
sort - swaps
Algorithm analysis
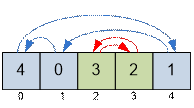
Let’s represent the
permutation as a union of cycles. The numbers inside one cycle of length k can be sorted in k – 1 swaps. For example, the permutation (4 0 3 2
1) splits into 2 cycles: (4 1 0) (3 2). Therefore, the permutation (4 0 3 2 1)
can be sorted in 2 + 1 = 3 swaps.
The sorted
permutation always has the form (0, 1, 2,…., n –
1), that is, the equality ai = i must hold. Let’s iterate over all possible
values of i and if ai ≠ i holds for some i, then using the swaps, sort the cycle to which belongs ai.
Algorithm realization
Store the
input permutation in the array a.
vector<int> a;
vector<pair<int, int> > ans;
Read the
input permutation.
scanf("%d", &n);
a.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);
If ai ≠ i, then
sort the numbers of the cycle which the number ai belongs to. Count the number
of swaps in the variable cnt.
for (i = 0; i < n; i++)
while (a[i] != i)
{
ans.push_back(make_pair(i,
a[i]));
swap(a[i], a[a[i]]);
cnt++;
}
Print the
number of swaps cnt and the swaps themselves.
printf("%d\n", cnt);
for (i = 0; i < ans.size(); i++)
printf("%d
%d\n", ans[i].first, ans[i].second);