8654. Целочисленное умножение

Даны три целых числа a, b, c. Вычислите значение выражения a ∗ b mod c.

Вход. Три целых положительных числа a, b, c (a, b, c < 2⁶³).

Выход. Выведите значение выражения a ∗ b mod c.

Пример входа	Пример выхода
1000000000007 10000000000005 1000000000000003	74970000000035

РЕШЕНИЕ

рекурсия

Анализ алгоритма

Задачу можно решить при помощи длинной арифметики на языке Java или Python. Однако здесь мы рассмотрим как решить задачу средствами языка программирования Си.

Пусть f(a, b, c) = (a ∗ b) mod c. Для вычисления функции воспользуемся рекурсией по аргументу b.

· Если b = 0, то (a ∗ 0) mod c = 0.

· Если b четно, то (a ∗ b) mod c = ((2 * a) mod c ∗ (b / 2)) mod c

· Если b нечетно, то (a ∗ b) mod c = (a ∗ (b – 1) + a) mod c

Таким образом

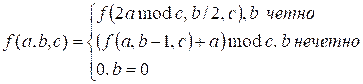
Поскольку a, b, c < 2⁶³, а при вычислениях используется только умножение на 2, то 2a < 2⁶⁴, что помещается в беззнаковый 64 битный тип unsigned long long.

Реализация алгоритма

Реализуем функцию mult умножения двух чисел a и b по модулю c.

unsigned long long mult(unsigned long long a, unsigned long long b,

unsigned long long c)

{

if (b == 0) return 0;

if (b % 2 == 0) return mult((2 * a) % c, b / 2, c);

return (mult(a, b - 1, c) + a) % c;

}

Основная часть программы. Читаем входные данные.

scanf("%lld %lld %lld", &a, &b, &c);

Вычисляем и выводим ответ.

res = mult(a, b, c);

printf("%lld\n", res);