8735. Сортировщик поезда

На старой железнодорожной станции Вы все еще можете столкнуться с одним из последних оставшихся “сортировщиков поездов”. Сортировщик поезда – это работник железной дороги, единственной задачей которого является перестановка вагонов поездов. После того, как вагоны расположены в правильном порядке, все, что нужно будет сделать машинисту поезда, это сбросить вагоны, один за другим, на станциях, для которых предназначен груз.

Название “сортировщик поезда” происходит от первого человека, который выполнил эту задачу, на станции, расположенной рядом с железнодорожным мостом. Вместо вертикального открытия мост вращался вокруг колонны в центре реки. Повернув мост на 90 градусов, лодки могут пройти влево или вправо.

Первый сортировщик поезда обнаружил, что мост может эксплуатироваться максимум с двумя вагонами на нем. Повернув мост на 180 градусов, вагоны поменялись местами, что позволило ему переставить вагоны (как побочный эффект, вагоны затем повернулись в противоположном направлении, но вагоны поезда могут двигаться в любом направлении, так что кого это волнует).

Теперь, когда почти все железнодорожные сортировщики вымерли, железнодорожная компания хотела бы автоматизировать их работу. Частью программы, которая должна быть разработана, является процедура, которая определяет для данного поезда наименьшее количество перестановок местами двух смежных вагонов, необходимых для приведения в порядок поезда. Ваше задание – создать такую программу.

Вход. Содержит в первой строке количество тестов n. Каждый тест состоит из двух строк. Первая строка теста содержит целое число l (0 ≤ l ≤ 10000), определяющее длину поезда. Вторая строка теста содержит перестановку чисел от 1 до l, указывающих текущий порядок вагонов. Вагоны должны быть упорядочены таким образом, чтобы вагон 1 шел первым, затем вагон 2 и так далее. Вагон номер l должен идти последним.

Выход. Для каждого теста выведите предложение: “Optimal train swapping takes s swaps.”, где s – целое число.

Пример входа	Пример выхода
3 3 1 3 2 4 4 3 2 1 2 2 1	Optimal train swapping takes 1 swaps. Optimal train swapping takes 6 swaps. Optimal train swapping takes 1 swaps.

РЕШЕНИЕ

инверсии

Анализ алгоритма

Пусть массив m содержит входную перестановку – текущий порядок вагонов. Искомое минимальное количество перестановок равно числу инверсий в перестановке.

Инверсией называется такая пара чисел (m_i, m_j), что i < j но при этом m_i > m_j. То есть пара чисел образует инверсию, если они стоят не в правильном порядке.

Например в массиве m = {3, 1, 2} инверсии образуют пары (3, 1) и (3, 2). Пара (1, 2) инверсии не образует, так как числа 1 и 2 стоят относительно друг друга в правильном порядке.

Количество инверсий в массиве длины n можно посчитать при помощи двойного цикла: переберем все возможные пары (i, j) для которых 1 ≤ i < j ≤ n, и если m_i > m_j, то имеем плюс одну инверсию.

Пример

Рассмотрим пример подсчета инверсий в перестановке. Под каждым числом запишем количество инверсий, которое оно образует с элементами правее него. Пусть inv[i] содержит количество таких j, что i < j и m[i] > m[j].

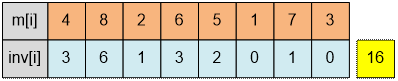
Общее количество инверсий равно 16.

Упражнение

Промоделируйте решение для следующего примера.

Реализация алгоритма

Объявим массив m.

int m[100010];

Последовательно обрабатываем тесты к задаче.

scanf("%d", &tests);

while (tests--)

{

Входной порядок вагонов читаем в массив m.

scanf("%d", &n);

for (i = 0; i < n; i++)

scanf("%d", &m[i]);

Минимальное количество перестановок для приведения в порядок поезда подсчитываем в переменной res.

res = 0;

for (i = 0; i < n - 1; i++)

for (j = i + 1; j < n; j++)

if (m[i] > m[j]) res++;

Выводим ответ.

printf("Optimal train swapping takes %lld swaps.\n", res);

}