8735. Train swapping
At the old railway station, you can still encounter one of the last
remaining train sorters. A train sorter is a railway
worker whose sole task is to rearrange train cars. Once the cars are in the
correct order, the train driver only needs to sequentially deliver them to the
stations for which the cargo is intended.
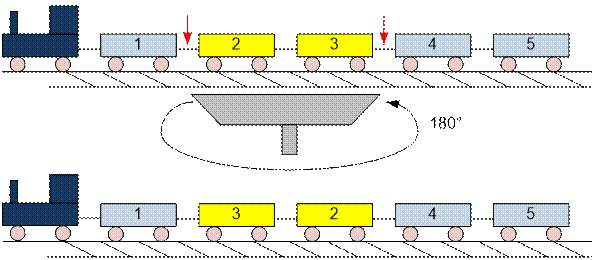
The name “train sorter” comes from the first person who performed this
task at a station located next to a railway bridge. Instead of opening
vertically, the bridge rotated around a column in the center of the river. By
turning the bridge by 90 degrees, boats could pass either to the left or to the
right.
The first train sorter discovered that the bridge could hold at most two
cars at a time. By rotating the bridge by 180 degrees, the cars swapped places,
allowing him to rearrange them (as a side effect, the cars then ended up facing
the opposite direction, but since trains can move in any direction, this was
not a problem).
Now, with almost all railway sorters extinct, the railway company aims
to automate their work. Part of the program that must be developed is a
procedure that determines, for a given train, the minimum number of swaps of
two adjacent cars required to put the train in the correct order. Your task is
to create such a program.
Input. The first line contains the number of test cases n. Each test case consists of two lines. The first line of a test
case contains an integer l (0 ≤
l ≤ 10000) – the length of the
train. The second line contains a permutation of the numbers from 1 to l representing the current order of the
cars. The cars must be ordered so that car 1 comes first, then car 2, and so
on, with car l last.
Output. For each test case, print the sentence: “Optimal train swapping takes s swaps.”, where s is an integer representing the minimum number of swaps needed.
|
Sample
input |
Sample
output |
|
3 3 1 3 2 4 4 3 2 1 2 2 1 |
Optimal train swapping takes 1 swaps. Optimal train swapping takes 6 swaps. Optimal train swapping takes 1 swaps. |
SOLUTION
inversions
Algorithm analysis
Let the
array m contain
the input permutation – the
current order of the train cars. The
desired minimum number of swaps is equal to the number of inversions in this
permutation.
An inversion is a pair of elements (mi, mj) such that i
< j but mi > mj.
In other words, a pair of elements forms an inversion if they are arranged in
the wrong order.

For
example, in the array m = {3, 1, 2}, the pairs (3, 1) and (3, 2) form
inversions. The pair (1, 2) does not form an inversion since the numbers 1 and 2 are in the
correct relative order.
The number
of inversions in an array of length n can be
counted using a double loop: iterate
over all possible pairs (i, j) such that 1 ≤ i
< j ≤ n, and if mi > mj, increase
the inversion counter by one.
Example
Let us
consider an example of counting inversions in a permutation. Under each number, we’ll write the number of inversions it forms with the
elements to its right. Let inv[i] denote the
number of indices j such that i < j and m[i] > m[j].
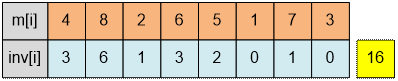
The total
number of inversions is 16.
Exercise
Simulate the solution for the
following example.

Algorithm
implementation
Declare the array m.
int m[100010];
Sequentially
process all tests test
cases.
scanf("%d", &tests);
while (tests--)
{
Read the input order of the train cars into the
array m.
scanf("%d", &n);
for (i = 0; i <
n; i++)
scanf("%d", &m[i]);
The minimum number of swaps required to arrange
the train in order is computed and stored in the variable res.
res = 0;
for (i = 0; i <
n - 1; i++)
for (j = i + 1; j
< n; j++)
if (m[i] >
m[j]) res++;
Print the answer.
printf("Optimal
train swapping takes %lld swaps.\n", res);
}