8761. Depth first search –
timestamps
Undirected graph is
given. Run depth first search from the given vertex v. Print the
timestamps d[v] and f[v] for each vertex v in the
increasing order of vertices.
Input. First line
contains number of vertices n (n ≤ 100) and edges m of
undirected graph. Each of the next m lines contains two
vertices a and b – an undirected edge of the
graph. The last line contains vertex v.
Output. Run dfs(v).
Print the timestamps d[v] and f[v] for each
vertex v (v = 1, 2, ..., n).
The timestamps for each vertex must be printed in a separate line.
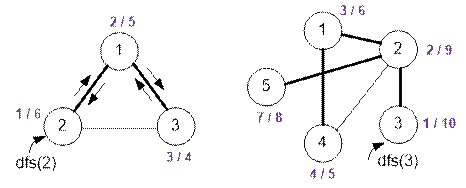
|
Sample input 1 |
Sample output 1 |
|
3 3 1 2 2 3 1 3 2 |
2 5 1 6 3 4 |
|
|
|
|
Sample input 2 |
Sample output 2 |
|
5 5 1 2 2 3 2 5 2 4 1 4 3 |
3 6 2 9 1 10 4 5 7 8 |
SOLUTION
graphs
– depth first search
Algorithm analysis
Let’s construct an adjacency matrix from the list of edges.
Run the depth-first search
from the given vertex v. Store the values of the labels into arrays d and f.
Algorithm
realization
Declare an adjacency matrix g, an array of lamps used, arrays d and f. Declare a time counter t.
#define MAX 101
int g[MAX][MAX], used[MAX];
int d[MAX], f[MAX];
int t;
The dfs function starts the
depth first search from the vertex v.
void dfs(int v)
{
Store the entry timestamp.
d[v] = t++;
Mark the vertex v as visited.
used[v] = 1;
Iterate through the vertices i where we can go
from v. We can go to the vertex i from v if there is
an edge between them (g[v][i] = 1) and vertex i is
not visited (used[i] = 0).
for (int i = 1; i <=
n; i++)
if ((g[v][i] == 1)
&& (used[i] == 0)) dfs(i);
Store the exit timestamp.
f[v] = t++;
}
The main part of the program. Read the number of
vertices n and edges m.
scanf("%d %d", &n, &m);
Initialize the arrays with zeroes.
memset(g,
0, sizeof(g));
memset(used,
0, sizeof(used));
Read the list of edges. Construct the adjacency
matrix.
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a][b] = g[b][a] = 1;
}
Read the vertex v, set time counter t = 1 and run the depth
first search from the vertex v.
scanf("%d", &v);
t
= 1;
dfs(v);
Print the timestamps d[i] and f[i] for each vertex i.
for (i = 1; i <= n; i++)
printf("%d
%d\n", d[i], f[i]);
Python realization
The dfs function starts the
depth first search from the vertex v.
def dfs(v):
The function uses the global variable t.
global t
Store the entry timestamp. Increase time t by 1.
d[v] = t
t
+= 1
Mark the vertex v as visited.
used[v] = True
Iterate over the vertices to where we
can go from v. It’s possible to go to the vertex to from v
if vertex to is not visited (used[to] = 0).
for
to in g[v]:
if not used[to]:
dfs(to)
Store the exit timestamp. Increase time t by 1.
f[v] = t
t
+= 1
The main part of the program. Read the number of
vertices n and edges m.
n, m = map(int, input().split())
Create the adjacency list g and the
list of lamps used.
g = [[] for _ in range(n+1)]
used = [False] * (n + 1)
Read the list of edges. Construct the adjacency
matrix.
for i in range(m):
a,
b = map(int, input().split())
g[a].append(b)
g[b].append(a)
Initialize the lists d and f.
d = [0] * (n + 1)
f = [0] * (n + 1)
Read the vertex v, set time counter t = 1 and run the depth
first search from the vertex v.
v = int(input())
t = 1
dfs(v)
Print the timestamps d[i] and f[i] for each vertex i.
for i in range(1, n+1):
print(d[i],f[i])