832. Increasing subsequence

Given n integers x₁, x₂, ..., x_n. Delete from them the least number of integers so that the rest were in ascending order.

Input. The first line contains the number n (1 ≤ n ≤ 10⁵). The second line contains the integers x₁, x₂, ..., x_n (1 ≤ x_i ≤ 60 000).

Output. Print in the first line the number of not erased integers. In the second line print the list of unerased integers in the original order. If several answers exist, print any.

Sample input	Sample output
6 2 5 3 4 6 1	4 2 3 4 6

SOLUTION

longest increasing subsequence

Algorithm analysis

The largest increasing subsequence must be found and printed.

For each element x_i (1 ≤ i ≤ n), find the length of the LIS that ends at x_i. Store these values in array L. This information is enough to find the LIS itself in linear time. The length of the LIS equals to the maximum number k in array L. Let this largest number k be in the index pos. Then the LIS ends with the number x_pos. Decrease pos until L[pos] becomes equal to k – 1. The current x_pos will be the penultimate element in the LIS. And so on, we continue to move the pos index to the start of array L, stopping at the first positions for which L[pos] = k – 2, …, L[pos] = 0.

Theorem. Consider the indices i₁ < i₂ < …< i_m, for which L[i₁] = L[i₂] = …= L[i_m]. Then the sequence x_i1, x_i2, …, x_im is decreasing.

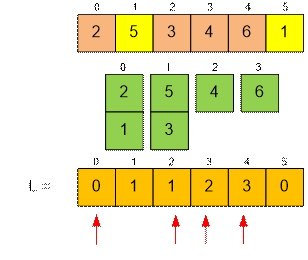
Example

The solitaire layout looks like:

L[i] contains the number of the pile where the card x_i will be placed (the piles are numbered starting from zero).

Algorithm realization

Declare the arrays.

#define MAX 60001

int x[MAX], lis[MAX], L[MAX];

Print the LIS.

void PrintSeq(int pos)

{

if (size < 0) return;

while(L[pos] != size) pos--;

size--; PrintSeq(pos-1);

printf("%d ",x[pos]);

}

The main part of the program. Read the input sequence.

scanf("%d",&n);

for(i = 0; i < n; i++)

scanf("%d",&x[i]);

Fill the arrays.

for (len = i = 0; i < n; i++)

{

pos = lower_bound(lis,lis+len,x[i]) - lis;

lis[pos] = x[i];

L[i] = pos;

if (pos == len) len++;

}

Print the largest increasing subsequence.

printf("%d\n",len); size = len - 1;

PrintSeq(n-1);

printf("\n");