877. Головоломка умножения

В головоломку умножения играют с рядом карт, каждая из которых содержит одно положительное целое число. Во время хода игрок убирает одну карту из ряда и получает число очков, равное произведению числа на убранной карте и чисел на картах, лежащих непосредственно слева и справа от неё. Не разрешено убирать первую и последнюю карты ряда. После последнего хода в ряду остаётся только две карты.

Цель игры – убрать карты в таком порядке, чтобы минимизировать общее количество набранных очков.

Например, если карты содержат числа 10, 1, 50, 20 и 5, игрок может взять карту с числом 1, затем 20 и 50, получая очки

10 * 1 * 50 + 50 * 20 * 5 + 10 * 50 * 5 = 500 + 5000 + 2500 = 8000

Если бы он взял карты в обратном порядке, то есть 50, затем 20, затем 1, количество очков было бы таким:

1 * 50 * 20 + 1 * 20 * 5 + 10 * 1 * 5 = 1000 + 100 + 50 = 1150.

Вход. В первой строке находится количество карт n, во второй – n (3 ≤ n ≤ 100) чисел на картах. Все числа на картах целые от 1 до 100.

Выход. Вывести одно целое число – минимально возможное число очков.

Пример входа	Пример выхода
6 10 1 50 50 20 5	3650

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Входную последовательность карт занесем в массив a[0, …, n – 1]. Пусть f(i, j) – наименьшее количество баллов, которое можно получить, удалив все карты строго внутри отрезка [a_i, …, a_j] (кроме крайних двух a_i и a_j, крайние карты по условию задачи удалять нельзя). Сохраним это значение в ячейке dp[i][j].

Тогда ответом на задачу будет f(0, n – 1).

Занесем в ячейки массива dp значения INF = ∞, инициализируем f(i, i) = dp[i][i] = 0, f(i, i + 1) = dp[i][i + 1] = 0.

Предположим, что при убирании чисел внутри отрезка [a_i, …, a_j] последним будет убрано a_k (i < k < j). При этом оно в общую сумму принесет слагаемое a_i a_k a_j. Но для того чтобы a_k на последнем шаге выбора карты было соседним с a_i и a_j, необходимо перед этим убрать все карты внутри отрезков [a_i, …, a_k] и [a_k, …, a_j]. То есть

f(i, j) =

Например,

f(i, i + 2) = f(i, i + 1) + f(i + 1, i + 2) + a_i * a_i+1 * a_i+2 = a_i * a_i+1 * a_i+2

Пример

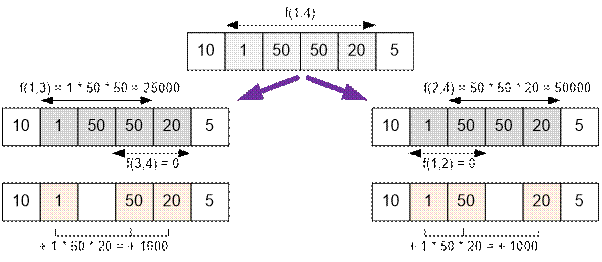
f(1, 4) = min( f(1, 3) + f(3, 4) + 1 * 50 * 20,

f(1, 2) + f(2, 4) + 1 * 50 * 20) =

= min( 0 + 50000 + 1000, 2500 + 0 + 1000) = 3500

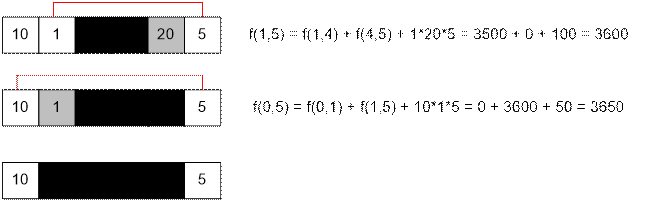
Значения f(i, j) = dp[i][j] приведем ниже:

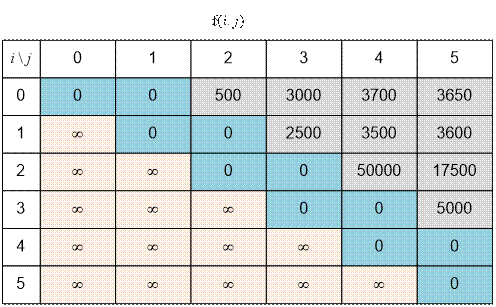
Ответ равен f(0, 5) = 3650.

Упражнение

Рассмотрим следующий пример. Пусть нам извесны такие даные.

· Вычислите значние f(0, 5).

· Заполните таблицу для массива (5, 3, 4, 1, 6, 2):

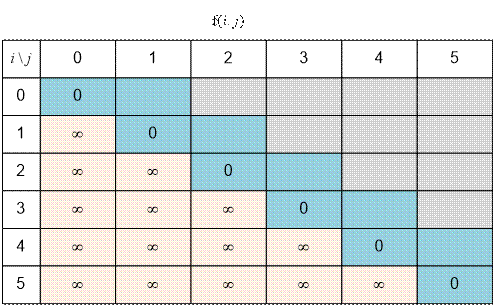
Реализация алгоритма

Объявим рабочие массивы.

#define MAX 110

#define INF 0x3F3F3F3F

int dp[MAX][MAX], a[MAX];

Функция f(i, j) возвращает наименьшее количество баллов, которое можно получить, удалив все карты строго внутри отрезка [a_i, …, a_j] (кроме крайних двух a_i и a_j, крайние карты по условию задачи удалять нельзя).

int f(int i, int j)

{

if (dp[i][j] == INF)

for (int k = i + 1; k < j; k++)

dp[i][j] = min(dp[i][j], f(i,k) + f(k,j) + a[i] * a[k] * a[j]);

return dp[i][j];

}

Основная часть программы. Читаем входные данные. Инициализируем массив dp.

scanf("%d",&n);

memset(dp,0x3F,sizeof(dp));

for(i = 0; i < n; i++)

{

scanf("%d",&a[i]);

dp[i][i] = 0;

dp[i][i+1] = 0;

}

Вычисляем и выводим ответ.

printf("%d\n",f(0,n-1));

Java реализация

import java.util.*;

public class Main

{

static int dp[][], a[];

public static int f(int i, int j)

{

if (dp[i][j] == Integer.MAX_VALUE)

for (int k = i + 1; k < j; k++)

dp[i][j] = Math.min(dp[i][j], f(i,k) + f(k,j) + a[i] * a[k] * a[j]);

return dp[i][j];

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

dp = new int[n][n];

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

dp[i][j] = Integer.MAX_VALUE;

a = new int[n];

for(int i = 0; i < n; i++)

{

a[i] = con.nextInt();

dp[i][i] = 0;

if (i < n - 1) dp[i][i+1] = 0;

}

int res = f(0, n - 1);

System.out.println(res);

con.close();

}

}