877. Puzzle
multiplication
In multiplication puzzle
play with a number of cards, each of which contains one positive integer.
During a turn a player removes one card from the series and gets the number of
points equal to the product number on the cleaned card and the numbers on the
cards, lying immediately to the left and right of it. Are not allowed to remove
the first and last card number. After the last course in the series remains the
only two cards.
Goal of the game – to
remove cards in such a manner as to minimize the total number of points.
For example, if the cards
contain numbers 10, 1, 50, 20 and 5, the player can take the card with the
number 1, then 20 and 50, get points
10 * 1 * 50 + 50 * 20 * 5
+ 10 * 50 * 5 = 500 + 5000 + 2500 = 8000
If he took the cards in
reverse order, i.e. 50, then 20, then 1, the number of points would be:
1 * 50 * 20 + 1 * 20 * 5 +
10 * 1 * 5 = 1000 + 100 + 50 = 1150.
Input. The first line is the number of cards n (3 ≤ n ≤
100), the second – n numbers on the
cards. The numbers on the cards are integers from 1 to 100.
Output. Print a single integer –
the minimum possible number of points.
|
Sample
input |
Sample
output |
|
6 10 1 50 50 20 5 |
3650 |
SOLUTION
dynamic programming
Algorithm analysis
Put the input sequence of
cards into array a[0, …, n – 1]. Let f(i, j)
be the smallest number of points that can be obtained by removing all cards
strictly inside the segment [ai,
…, aj] (except for the
extreme two ai and aj, the extreme cards cannot
be removed by the problem statement). Store this value in dp[i][j].

Then the answer to the
problem will be f(0, n – 1).
Put the values INF =
∞ into the cells of dp array, initialize f(i, i) = dp[i][i]
= 0, f(i, i + 1) = dp[i][i + 1] = 0.
Suppose that when removing
numbers inside the segment [ai,
…, aj], the last will be
removed ak (i < k < j). Moreover, it
will add to the total sum the term ai
ak aj. But in order for ak to be adjacent to ai
and aj at the last step of
choosing a card, it is necessary to remove all cards inside the segments [ai, …, ak] and [ak,
…, aj]. I.e
f(i, j)
= ![]()

For example,
f(i,
i + 2) = f(i, i + 1) + f(i + 1, i + 2) + ai * ai+1 * ai+2 = ai * ai+1 * ai+2
Example
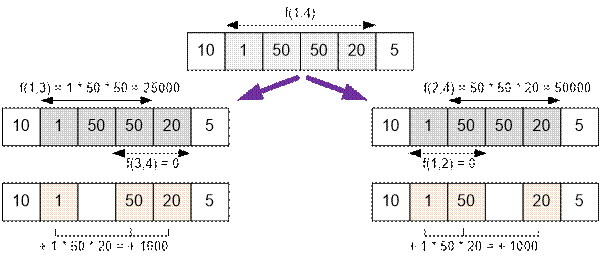
f(1, 4) = min( f(1, 3) +
f(3, 4) + 1 * 50 * 20,
f(1, 2) + f(2, 4) +
1 * 50 * 20) =
= min( 0 + 50000 + 1000,
2500 + 0 + 1000) = 3500
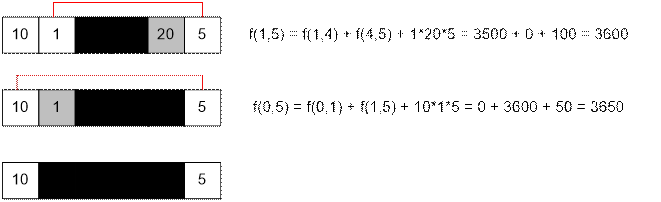
The values of f(i, j)
= dp[i][j] are given below:
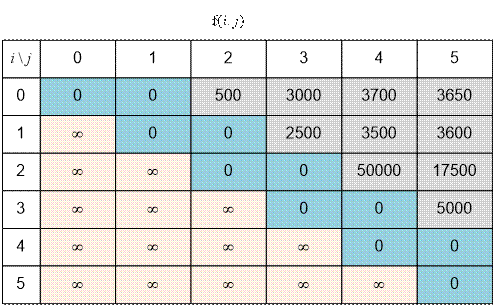
The answer is f(0, 5) =
3650.
Exercise
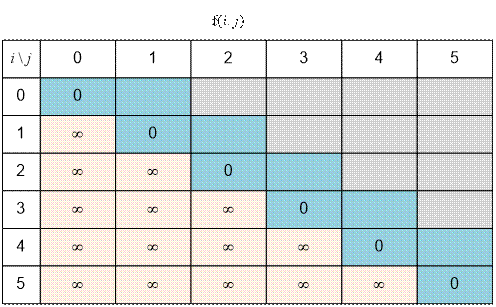
Consider the following
example. Suppose we are given the following data.

·
Compute the value of f(0, 5).
·
Fill the table for the array (5, 3, 4, 1, 6, 2):
Algorithm realization
Declare the arrays.
#define MAX 110
#define INF
0x3F3F3F3F
int
dp[MAX][MAX], a[MAX];
Function f returns the smallest number of points that can be obtained by
removing all cards strictly inside the segment [ai, …, aj]
(except for the extreme two ai
è aj, the extreme cards cannot
be removed by the problem statement).
int f(int i, int j)
{
if (dp[i][j] == INF)
for (int k = i + 1; k
< j; k++)
dp[i][j] = min(dp[i][j], f(i,k) + f(k,j) + a[i] * a[k] * a[j]);
return dp[i][j];
}
The main part of the program. Read the input data. Initialize the dp
array.
scanf("%d",&n);
memset(dp,0x3F,sizeof(dp));
for(i = 0; i
< n; i++)
{
scanf("%d",&a[i]);
dp[i][i] = 0;
dp[i][i+1] = 0;
}
Compute and print the answer.
printf("%d\n",f(0,n-1));
Java realization
import java.util.*;
public class Main
{
static int dp[][], a[];
public static int f(int i, int j)
{
if (dp[i][j] == Integer.MAX_VALUE)
for (int k = i + 1; k < j; k++)
dp[i][j] = Math.min(dp[i][j], f(i,k) + f(k,j) + a[i] * a[k] * a[j]);
return dp[i][j];
}
public static void main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
dp = new int[n][n];
for(int i = 0; i < n; i++)
for(int j = 0; j < n; j++)
dp[i][j] = Integer.MAX_VALUE;
a = new int[n];
for(int i = 0; i < n; i++)
{
a[i] = con.nextInt();
dp[i][i] = 0;
if (i < n - 1) dp[i][i+1] = 0;
}
int res = f(0, n - 1);
System.out.println(res);
con.close();
}
}