9006. Пройти
через реку
Барыш и Мурад работают
надсмотрщиками в отделе надсмотра за животными Бакинского зоопарка. Очень часто
им приходится решать задачи сложнее задачи крестьянина. Например, однажды,
использую только две лодки они должны были перевести всех животных зоопарка через
реку Кура. Представьте себя на их месте.
В зоопарке имеются n животных.
Если оставить некоторых животных вместе без присмотра, то один из них может
съесть другого. Для каждого животного известно каких других животных он может
съесть. Оба надсмотрщика мастера своего дела и могут справиться даже с тигром!
Любое животное не сможет съесть другое животное, если рядом находится
надсмотрщик.
У надсмотрщиков имеются две
лодки. По правилам безопасности, нельзя брать в лодку двух или более животных.
В каждой из лодок одновременно могут находиться самое большее один надсмотрщик
и одно животное. В самом начале все животные и надсмотрщики находятся по левую
сторону реки. Им всем надо перейти на правую сторону. (Очевидно, что у реки
имеются только две стороны)
Надсмотрщики могут переплывать
через реку в любом направлении. Лодки не могут двигаться без надсмотрщиков. В
любой момент если на одной из сторон останутся животные без присмотра которые
могут съесть друг друга, то произойдет несчастный случай. Естественно, это не
допустимо. Все животные должны перейти на другую сторону реки целыми и
невредимыми.
От вас требуется выяснить,
возможно ли это.
Вход. В первой строке дано одно целое
число n (1 ≤ n ≤ 200) – количество животных в
зоопарке. Животные пронумерованы различными числами от 1 до n.
В каждой из последующих n строк,
для каждого животного, дан список животных которые могут съесть это животное. В
i-той строке для животного с номером i дается сначала
неотрицательное целое число ki – количество животных, которые
могут съесть это животное, далее следуют ki различных чисел –
номера этих животных. Все эти числа находятся в промежутке от 1 до n
и отличны от i (никакое животное не может съесть самого себя).
Сумма всех ki не
больше 1500.
Выход. Если возможно перевести всех
животных на другую сторону реки, выведите ":)", в противном случае
выведите ":(".
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 3 3 2 4 1 1 1 1 1 1 |
:) |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 4 2 5 3 4 4 3 1 4 5 4 1 5 2 4 4 1 5 3 2 4 4 2 1 3 |
:( |
РЕШЕНИЕ
поиск в
глубину
Анализ алгоритма
Каждому животному поставим в
соответствие вершину графа. Если одно животное может съесть другое, проведем
между ними ребро.
Пока один из надсмотрщиков
остается на первом берегу с животными, второй начинает перевозить на второй
берег тех, кто друг друга не ест. Предположим, что наступает момент, когда
очередную такую перевозку совершить невозможно. Тогда два надсмотрщика берут с
первого берега по животному себе в лодку и перевозят на второй берег. При этом
должно выполняться условие:
·
Ни на первом, ни на втором берегу животные не должны есть друг друга. То
есть после удаления двух вершин (двое животных что в лодках надсмотрщиков) граф
должен быть двудольным.
Далее после перевоза двух животных
на второй берег, один из надсмотрщиков остается там беречь животных, а второй
начинает перевозить оставшихся на первом берегу животных.
Таким образом животных можно
перевезти на второй берег реки, если найдутся такие две вершины графа (двое
животных), что удалив их, граф станет двудольным. Осталось перебрать все возможные
пары вершин и проверить граф на двудольность.
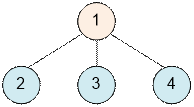
Пример
В первом примере граф даже без
удаления вершин уже является двудольным.
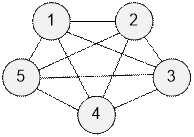
Во втором примере граф является
полным и невозможно удалить две вершины так чтобы он стал двудольным.
Реализация алгоритма
Объявим матрицу смежности g и массив использованных вершин used.
#define MAX 202
int g[MAX][MAX];
int used[MAX];
Функция dfs совершает поиск в глубину из вершины v. Вершину v красим цветом color.
void dfs(int v, int color = 1)
{
Если граф не двудольный (flag =
1), то нет смысла продолжать поиск в глубину.
if (flag == 1) return;
Красим вершину v цветом color.
used[v] = color;
Перебираем вершины, куда можно пойти
из v.
for (int i = 1; i <= n; i++)
if (g[v][i] == 1)
{
Двигаемся по ребру (v,
i). Если вершина i не пройдена, то запускаем из нее
поиск в глубину. Красим вершину i цветом 3 – color.
if (used[i] == 0) dfs(i, 3
- color); else
Если цвет вершин v и i совпадает, значит ребро (v,
i) обратное
и граф не двудольный. Устанавливаем flag =
1.
if (used[v] == used[i]) flag = 1;
}
}
Основная часть программы. Читаем
входные данные. Строим граф.
scanf("%d", &n);
for (i = 1; i <= n; i++)
{
scanf("%d", &k);
while (k--)
{
scanf("%d", &j);
g[i][j] = g[j][i] = 1;
}
}
Если животных не более 4, то их
всегда можно перевезти.
if (n <= 4)
{
puts(":)");
return 0;
}
Перебираем пару животных (i, j).
for (i = 1; i <= n; i++)
for (j = i + 1; j <= n; j++)
{
memset(used, 0, sizeof(used));
Удаляем животных с номерами i и j и не рассматриваем их при поиске в глубину.
used[i] = used[j] = 3;
Изначально положим flag =
0 считая граф двудольным.
flag = 0;
Граф не обязательно связный.
Запускаем поиск в глубину на несвязном графе.
for (k = 1; k <= n; k++)
if (used[k] == 0)
{
dfs(k);
Если после обработки очередной
компоненты связности компонента не является двудольной, то нет смысла далее продолжать
поиск в глубину.
if (flag == 1) break;
}
Если граф двудольный, то перевозка
животных возможна.
if (flag == 0)
{
puts(":)");
return 0;
}
}
Перевезти животных невозможно.
puts(":(");