9018. n-th integer divisible by a or b
Given two positive
integers a and b. Find the n-th positive
integer that is divisible by either a
or b.
Input. Three positive integers a, b and n (a, b, n ≤ 109).
Output. Print the n-th positive integer that is divisible
by either a or
b. It is guaranteed that this number
does not exceed 109.

|
Sample
input 1 |
Sample
output 1 |
|
2 5 10 |
16 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
3 7 25 |
57 |
SOLUTION
binary search
Algorithm analysis
Let the function f(n) compute the
number of positive integers in the range [1; n] that are divisible by either a or b. This value can be computed using the formula:
n / a + n
/ b – n / LCM(a, b)
Let x
be the n-th number that is divisible
by either a or b. Then x is the smallest positive integer such
that f(x) = n. We will find x using binary search on the
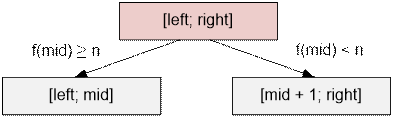
interval [left; right] = [1; 109]. At each step, compute mid = (left + right) / 2. If f(mid) ≥ n, continue searching in the left subinterval [left; mid]; otherwise, search in the right subinterval [mid + 1; right].
Example
Consider the first example where a = 2 and b = 5. We
need to find the smallest value of x such
that f(x) = 10. Let’s compute the
values of the function f(x) for some values of x.
·
f(15)
= 15 / 2 + 15 / 5 – 15 / 10 = 7 + 3 – 1 = 9;
·
f(16)
= 16 / 2 + 16 / 5 – 16 / 10 = 8 + 3 – 1 = 10;
·
f(17)
= 17 / 2 + 17 / 5 – 17 / 10 = 8 + 3 – 1 = 10;
·
f(18)
= 18 / 2 + 18 / 5 – 18 / 10 = 9 + 3 – 1 = 11;
The smallest solution to the equation f(x)
= 10 is x = 16.
Algorithm implementation
The functions gcd and lcm compute the greatest common divisor and the
least common multiple, respectively.
long long gcd(long long a, long long b)
{
return (b == 0) ? a : gcd(b, a % b);
}
long long lcm(long long a, long long b)
{
return a /
gcd(a, b) * b;
}
The function f(n) returns the
number of positive integers less than or equal to n that are divisible by either a or b.
long long f(long long n)
{
return n / a
+ n / b - n / lcm(a, b);
}
Read the input data.
scanf("%lld %lld %lld",
&a, &b, &n);
Perform a binary search on the interval [left; right] = [1; 109]. The goal is to find the smallest value of left such that f(left) = n.
left = 1; right = 1e9;
while (left < right)
{
middle
= (left + right) / 2;
if
(f(middle) >= n)
right
= middle;
else
left
= middle + 1;
}
Print the answer.
printf("%lld\n",
left);
Java implementation
import java.util.*;
import java.io.*;
public class Main
{
static long gcd(long a, long b)
{
return (b ==
0) ? a : gcd(b, a % b);
}
static long lcm(long a, long b)
{
return a / gcd(a, b) * b;
}
static long f(long n, long a, long b)
{
return n / a + n / b - n / lcm(a, b);
}
public static void
main(String[] args)
{
FastScanner con = new
FastScanner(new InputStreamReader(System.in));
long a = con.nextInt();
long b = con.nextInt();
long n = con.nextInt();
long left = 1,
right = 1000000000;
while (left <
right)
{
long middle = (left + right) /
2;
if (f(middle, a, b)
>= n)
right = middle;
else
left = middle + 1;
}
System.out.println(left);
}
}
class FastScanner
{
private BufferedReader br;
private StringTokenizer st;
public
FastScanner(InputStreamReader reader)
{
br = new BufferedReader(reader);
}
public
String next()
{
while (st == null || !st.hasMoreTokens())
{
try
{
st = new StringTokenizer(br.readLine());
} catch
(Exception e)
{
e.printStackTrace();
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
public void
close() throws Exception
{
br.close();
}
}