9019. n-ое число, делящееся на a, b или c
Даны три числа a, b
и с. Найдите n-ое число, которое делится либо
на a, либо на b,
либо на c.
Вход. Четыре
натуральных числа a, b, c
и n (a, b, c, n ≤ 109).
Выход. Выведите n-ое число, которое делится либо
на a, либо на b,
либо на c. Известно, что оно не
более 109.

|
Пример
входа 1 |
Пример
выхода 1 |
|
2 3 5 10 |
14 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
3 5 7 10 |
18 |
РЕШЕНИЕ
бинарный
поиск
Анализ алгоритма
Пусть функция f(n) вычисляет количество натуральных чисел на промежутке [1;
n], делящихся или
на a, или на b, или на c. Это количество равно
n / a + n / b + n
/ c –
n / НОК(a, b)
– n / НОК(a, c)
– n / НОК(b, c)
+ n / НОК(a, b,
c)
Пусть x – искомое n-ое число.
Тогда x должно быть таким наименьшим
натуральным числом, что f(x) = n. Его будем искать бинарным
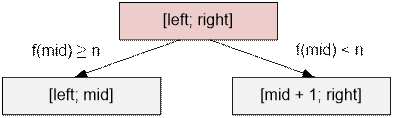
поиском, начиная с отрезка [left; right] = [1; 109]. Пусть mid = (left + right) / 2. Если f(mid)
≥ n, то поиск следует продолжать на отрезке [left;
mid], иначе –
на отрезке [mid + 1; right].
Пример
Рассмотрим
первый пример, в котором a = 2, b = 3, c = 5. Необходимо найти наименьшее x, для которого f(x) =
10. Вычислим некоторые значения:
·
f(13)
= 13 / 2 + 13 / 3 + 13 / 5 – 13 / 6 – 13 / 10 – 13 / 15 + 13 / 30 =
6 + 4 + 2 – 2 – 1 – 0 + 0 = 9;
·
f(14)
= 14 / 2 + 14 / 3 + 14 / 5 – 14 / 6 – 14 / 10 – 14 / 15 + 14 / 30 =
7 + 4 + 2 – 2 – 1 – 0 + 0 = 10;
·
f(15)
= 15 / 2 + 15 / 3 + 15 / 5 – 15 / 6 – 15 / 10 – 15 / 15 + 15 / 30 =
7 + 5 + 3 – 2 – 1 – 1 + 0 = 11;
Наименьшим решением уравнения f(x)
= 10 будет x = 14.
Реализация алгоритма
Функции вычисления НОД и НОК.
long long gcd(long long a, long long b)
{
return (b == 0) ? a : gcd(b, a % b);
}
long long lcm(long long a, long long b)
{
return a /
gcd(a, b) * b;
}
Функция f(n) возвращает количество натуральных чисел, не больших n, делящихся или на a, или на b, или на c.
long long f(long long n)
{
long long res = n / a
+ n / b + n / c –
n / lcm(a, b) - n /
lcm(a, c) - n / lcm(b, c);
long long temp = lcm(a, b);
if
(temp < 1000000000) res += n /
lcm(temp, c);
return res;
}
Читаем входные данные.
scanf("%lld %lld %lld %lld",
&a, &b, &c, &n);
Запускаем бинарный поиск. Ищем
наименьшее значение left, для которого f(left)
= n.
left = 1; right = 1e9;
while (left < right)
{
middle
= (left + right) / 2;
if
(f(middle) >= n)
right
= middle;
else
left
= middle + 1;
}
Выводим ответ.
printf("%lld\n",
left);