9020. Split into k sub-arrays
An array of n elements and a number k are
given. Split the array into k subarrays, using all elements of
the original array (the order of elements must be preserved, and each element
must belong to exactly one subarray).
For each such
partition, compute the maximum of the sums of
the k subarrays. Your task is to perform the partitioning in
such a way that this maximum is as small as possible. Find the minimum possible
value of this maximum.
Input. The first line
contains two integers n and k (1 ≤ k
≤ n ≤ 106).
The second line
contains n positive integers – the elements of
the array. Each number does not exceed 109.
Output. Print the
smallest possible value of the maximum sum among all valid partitions of the
array into k subarrays.
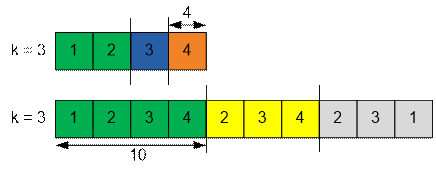
Explanation. In the first example, an
optimal partition is: {1, 2}, {3}, {4}. The subarray sums are: 3, 3, 4.
The maximum among them is 4, which is the smallest possible value
for k = 3.
In the second
example, an optimal partition is: {1, 2, 3, 4}, {2, 3, 4}, {2, 3, 1}. The
subarray sums are: 10, 9, 6. The maximum is 10, which is
the smallest possible value for k = 3.
|
Sample
input 1 |
Sample
output 1 |
|
4
3 1
2 3 4 |
4 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
10
3 1
2 3 4 2 3 4 2 3 1 |
10 |
SOLUTION
binary search
Algorithm analysis
We’ll search for the optimal value using
binary search. Obviously, this value cannot be less than 1 (since the elements
of the array are positive integers) and cannot exceed the sum of all elements
in the array. Set the boundaries: left = 1, right
= sum of all array elements. The answer is guaranteed to lie within the range [left;
right].
Now consider a helper subproblem: is it
possible to split the array into k subarrays such that the maximum sum
among all k subarrays does not exceed a given value s0? If the array contains at least one element greater
than s0, such a split is
impossible. Otherwise, we sequentially form subarrays so that the sum of each
does not exceed s0. If the
total number of resulting subarrays is no more than k, then such a split
is considered possible.
Example
In the second example, let us consider
possible ways to split the array into subarrays for different values of s0:



Algorithm implementation
Define a constant MAX = 106 and an array m.
#define MAX
1000000
int m[MAX];
The
function f returns 1 if the array can be split into k
subarrays such that the maximum sum among all k subarrays does not
exceed the given value s0.
int f(long long s0)
{
long long sum
= 0;
int cnt
= 1;
for (int i =
0; i < n; i++)
{
If any
element of the array is greater than s0, such a split is not possible.
if
(m[i] > s0) return 0;
Compute the
sum of the current subarray.
sum +=
m[i];
As soon as
this sum exceeds the value s0, increase the subarray counter cnt by 1 and
start accumulating the sum for the next subarray.
if (sum
> s0)
{
sum =
m[i];
cnt++;
}
}
If the
array can be split into no more than k subarrays, then it can also be
split into exactly k subarrays (since k ≤ n).
if (cnt
<= k) return 1;
return 0;
}
The main
part of the program. Read the input data. In the variable right, compute
the sum of all elements in the array.
scanf("%d %d",
&n, &k);
left = 1; right = 0;
for (i = 0; i < n; i++)
{
scanf("%d", &m[i]);
right
+= m[i];
}
The desired minimum value of the maximum
subarray sum lies within the range [left;
right]. Perform a binary search on
this interval.
while (left < right)
{
mid =
(left + right) / 2;
if
(f(mid) == 1)
right
= mid;
else
left
= mid + 1;
}
Print the
answer.
printf("%lld\n",
left);