9021. Count the integers of the form 2^x * 3^y

 

Find the number of integers from the range [a, b] that can be represented as 2x * 3y (x ≥ 0, y ≥ 0).

 

Input. Consists of no more than 106 lines. Each line contains two integers a and b (0 ≤ a ≤ b ≤ 1018) that represents one query.

 

Output. For each query print in a separate line the number of integers from the range [a, b] inclusively that can be represented as 2x * 3y.

 

Sample input

Sample output

1 10

100 200

7

5

 

 

SOLUTION

binary search

 

Algorithm analysis

The number of integers of the form 2x * 3y, not greater than 1018, is not so much. Generate them in array v.

The amount of required numbers f(a, b) on a segment [a, b] is f(0, b) – f(0, a – 1). The query f(0, q) means the number of integers of the form 2x * 3y, not greater than q. We look for the answer using a binary search on array v.

 

Example

Generate all numbers of the form 2x * 3y , no more than 200.

 

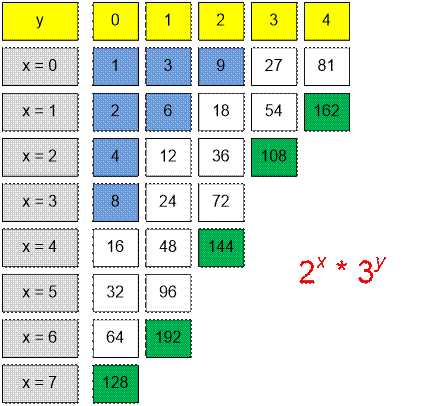
Segment [1; 10] contains 7 numbers (highlighted in blue).

Segment [100; 200] contains 5 numbers (highlighted in green).

 

Find a solution for segment [10; 20]:

upper_bound(v.begin(), v.end(), 20) – upper_bound(v.begin(), v.end(), 9) = 3

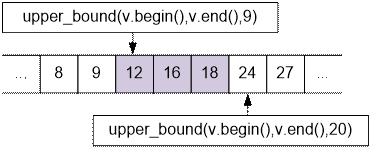
Indeed, segment [10; 20] contains 3 numbers of required form:

12, 16, 18

 

Algorithm realization

Declare the constant MAX = 1018. Declare the array v.

 

#define MAX 1000000000000000000LL

vector<long long> v;

 

Function preprocess generates all 2x * 3y numbers, not greater than 1018, in the v array. For each value x = 1, 2, 4, 8, … iterate over y = 1, 3, 9, 27, … until x * y < MAX.

 

void preprocess()

{

  long long x = 1, y = 1;

  while (x < MAX)

  {

    while (x * y < MAX)

    {

      v.push_back(x * y);

      y *= 3;

    }

    x *= 2;

    y = 1;

  }

 

Sort the numbers.

 

  sort(v.begin(), v.end());

}

 

The main part of the program. Generate the array of numbers of the form 2x * 3y.

 

preprocess();

 

Read the query – the segment [a, b]. The number of required numbers f(a, b) on segment [a, b] is f(0, b) – f(0, a – 1).

 

while (scanf("%lld %lld", &a, &b) == 2)

{

  res = upper_bound(v.begin(), v.end(), b) - upper_bound(v.begin(),

                    v.end(), a - 1);

  printf("%lld\n", res);

}