9023. Минимум увеличений

Задан массив из n натуральных чисел. Найдите наименьшее количество операций, необходимых для преобразования массива в арифметическую прогрессию с разностью 1.

За одну операцию разрешается увеличить любой элемент массива на 1.

Вход. Первая строка содержит одно целое число n (n ≤ 10⁶).

Вторая строка содержит n натуральных чисел, каждое из которых не превышает 10⁶.

Выход. Выведите наименьшее количество операций, необходимое для преобразования массива в арифметическую прогрессию с разностью 1.

Пояснение. В первом тесте массив следует преобразовать в

8 9 10 11 12

Для этого потребуется

(8 – 3) + (9 – 6) + (10 – 4) + (11 – 11) + (12 – 5) = 5 + 3 + 6 + 0 + 7 = 21

операция.

Пример входа 1	Пример выхода 1
5 3 6 4 11 5	21
Пример входа 2	Пример выхода 2
5 4 4 5 5 7	5

РЕШЕНИЕ

бинарный поиск

Анализ алгоритма

Пусть минимальное количество операций преобразует исходный массив

m[0], m[1], …, m[n – 1]

в арифметическую прогрессию вида

x, x + 1, x + 2, …, x + n – 1

Очевидно, что m[0] ≤ x ≤ max(m[0], m[1], …, m[n – 1]).

Назовём последовательность

d = [x, x + 1, x + 2, …, x + n – 1]

подходящей, если массив m можно преобразовать в d, то есть если выполняется условие m[i] ≤ d[i] для всех i от 0 до n – 1.

Остается найти наименьшее значение x, при котором последовательность d будет подходящей. Это можно сделать с помощью бинарного поиска.

Пример

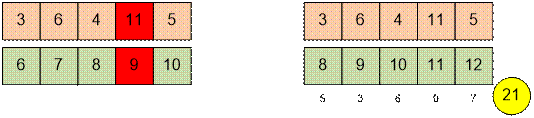
Рассмотрим первый тест. Пусть d = [x, x + 1, x + 2, …, x + n – 1] – подходящая последовательность с минимальной суммой элементов.

Очевидно, что m[0] = 3 ≤ x ≤ 11 = max(m[i]).

Бинарным поиском находим наименьшее значение x, при котором последовательность d является подходящей.

Например, при x = 6 последовательность d не будет подходящей, а при x = 8 будет.

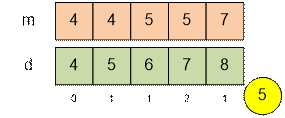
Рассмотрим второй тест. Бинарный поиск запускаем на промежутке 4 ≤ x ≤ 7. Например, уже при x = 4 последовательность d является подходящей.

Реализация алгоритма

Входную последовательность храним в массиве m. Последовательность x, x + 1, x + 2, …, x + n – 1 храним в массиве d.

#define MAX 1000000

int m[MAX], d[MAX];

Функция check генерирует в массиве d последовательность вида

first, first + 1, first + 2, …, first + n – 1

Если для каждого i (0 ≤ i ≤ n – 1) выполняется неравенство m[i] ≤ d[i], то массив d можно получить из массива m, увеличивая отдельные элементы на 1. В этом случае массив d называется подходящим.

Если массив d является подходящим, то функция check возвращает 1, в противном случае – 0.

int check(int first)

{

for (int i = 0; i < n; i++)

d[i] = first++;

for (int i = 0; i < n; i++)

if (m[i] > d[i]) return 0;

return 1;

}

Основная часть программы. Читаем входное значение n. Вычисляем максимальное значение mx в массиве m.

scanf("%d", &n);

mx = 0;

for (i = 0; i < n; i++)

{

scanf("%d", &m[i]);

if (m[i] > mx) mx = m[i];

}

start = m[0];

end = mx;

Запускаем бинарный поиск значения x в интервале [start; end] = [m[0]; mx].

Ищем минимальное значение x, при котором последовательность x, x + 1, x + 2, …, x + n – 1 может быть получена из массива m[0], m[1], …, m[n – 1].

while (start < end)

{

mid = (start + end) / 2;

if (check(mid))

end = mid;

else

start = mid + 1;

}

Генерируем искомую арифметическую прогрессию.

for (i = 0; i < n; i++)

d[i] = start++;

Вычисляем минимальное количество операций, необходимых для получения прогрессии.

op = 0;

for (int i = 0; i < n; i++)

op += (d[i] - m[i]);

Выводим ответ.

printf("%lld\n", op);