9032. Обновление
дорог
В Берляндии
есть n городов, соединённых m двусторонними дорогами. Дороги не
могут соединять город с самим собой, и между каждой парой городов может быть не
более одной дороги. При этом не гарантируется, что из любого города можно
попасть в любой другой, используя только существующие дороги.
Мэр города Гаджи Ибрагим решил
изменить систему дорожного сообщения и поручил министерству транспорта провести
реформу. Согласно новому плану, каждая дорога должна стать односторонней, то
есть вести только в одном направлении – из одного
города в другой.
Чтобы избежать недовольства
жителей, реформу необходимо провести так, чтобы число обособленных городов
оказалось минимальным. Город считается обособленным, если в него не входит ни
одна дорога (при этом дороги, выходящие из этого города, допустимы).
Помогите Гаджи Ибрагиму
определить минимальное возможное количество обособленных городов после
проведения реформы.
Вход. Первая строка содержит два натуральных числа n и m (2 ≤ n
≤ 105, 1 ≤ m ≤ 105) –
количество городов и дорог в Берляндии.
Далее в m строках описаны дороги: i-я
дорога задаётся двумя различными целыми числами xi и yi (1 ≤ xi, yi
≤ n, xi ≠ yi) – номерами городов, которые соединяет i-я дорога.
Гарантируется, что между каждой
парой городов не более одной дороги. Однако не гарантируется, что из любого
города можно добраться в любой другой по существующим дорогам.
Выход. Выведите одно число – минимальное количество
обособленных городов после проведения реформы.
|
Пример
входа 1 |
Пример
выхода 1 |
|
4 3 2 1 1 3 4 3 |
1 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
5 5 2 1 1 3 2 3 2 5 4 3 |
0 |
РЕШЕНИЕ
дерево
Анализ алгоритма
Рассмотрим неориентированный граф
и выделим в нём компоненты связности. Если компонента связности представляет
собой дерево (то есть не содержит циклов), ребра в ней всегда можно
ориентировать так, чтобы ровно одна вершина осталась без входящих рёбер. Это
означает, что в компоненте-дереве минимальное возможное количество обособленных
городов после реформы равно 1 (нулевое количество недостижимо). Например,
обособленным городом можно сделать корень дерева.
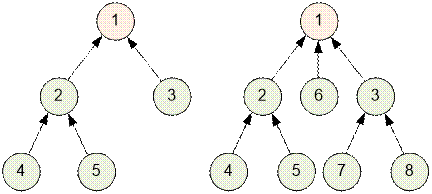
Если в компоненте связности
присутствует цикл, то ребра всегда можно ориентировать так, чтобы каждая
вершина имела хотя бы одно входящее ребро.
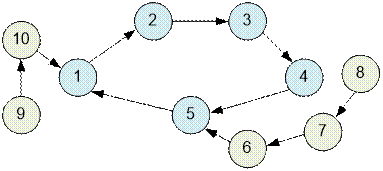
Ответом на задачу будет
количество компонент связности, не содержащих циклов.
Пример
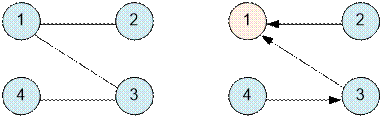
Рассмотрим первый пример. Слева показан
исходный граф, а справа – граф после реформы. Вершина 1 не имеет входящих
ребер.
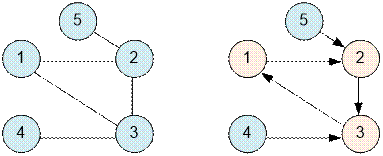
Рассмотрим второй пример. Слева показан
исходный граф, а справа – граф после реформы. В каждой вершине имеется по
одному входящему ребру.
Реализация алгоритма
Объявим список смежности g для хранения структуры
графа, а также массив used для отметки уже посещённых вершин.
vector<vector<int> > g;
vector<int>
used;
Функция dfs выполняет поиск в глубину,
начиная с вершины v. Предком вершины v является вершина p.
void dfs(int v, int p = -1)
{
used[v] = 1;
for (int to : g[v])
{
if (to == p) continue;
Если в текущей компоненте связности обнаруживается
цикл, устанавливаем flag =
0.
if (used[to] == 1) flag = 0;
else dfs(to, v);
}
}
Основная часть программы. Читаем
входные данные.
scanf("%d %d", &n, &m);
g.resize(n + 1);
used.resize(n + 1);
Читаем m ребер. Строим граф.
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Выполняем поиск в глубину на несвязном графе. В переменной
res хранится количество компонент связности, в которых нет циклов.
res = 0;
for (i = 1; i <= n; i++)
{
if (used[i] == 0)
{
Перед обработкой каждой компоненты устанавливаем flag
= 1. Если в процессе обхода будет обнаружен цикл, то после завершения вызова dfs
значение flag станет равным
0.
flag = 1;
dfs(i);
res += flag;
}
}
Выводим ответ.
printf("%d\n", res);