9032. Roads renewal
In Berland, there are n cities
connected by m bidirectional roads. Roads cannot connect a
city to itself, and there can be at most one road between any pair of cities.
It is not guaranteed that it is possible to travel from any city to any other
using only the existing roads.
The mayor of one city, Gadji Ibrahim,
decided to reform the road system and instructed the Ministry of Transport to
carry out the changes. Under the new plan, every road must become one-way,
meaning it will connect two cities in only one direction — from one city to
another.
To avoid public dissatisfaction, the reform
must be carried out so that the number of isolated cities is minimized. A city
is considered isolated if there are no roads entering it (outgoing roads from
such a city are allowed).
Help Gadji Ibrahim determine the minimum
possible number of isolated cities after the reform.
Input. The first line contains two positive integers n and
m (2 ≤ n ≤ 105, 1 ≤ m ≤ 105)
– the number of cities and the number of roads in Berland.
Each of the next m lines describes a
road: the i-th road is given by two distinct integers xi
and yi (1 ≤ xi, yi ≤
n, xi ≠ yi) – the indices
of the cities connected by the i-th road.
It is guaranteed that there is at most one
road between any pair of cities. However, it is not guaranteed that one can
travel from any city to any other using only the existing roads.
Output. Print a single integer – the minimum number of
isolated cities after the reform.
|
Sample
input 1 |
Sample output 1 |
|
4 3 2 1 1 3 4 3 |
1 |
|
|
|
|
Sample
input 2 |
Sample output 2 |
|
5 5 2 1 1 3 2 3 2 5 4 3 |
0 |
SOLUTION
tree
Algorithm analysis
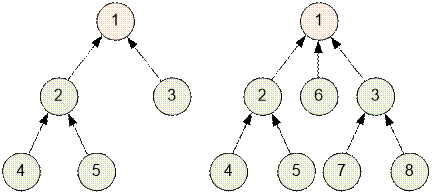
Consider an undirected graph and identify
its connected components. If a connected component is a tree (that is, it
contains no cycles), its edges can always be oriented so that exactly one
vertex has no outgoing edges. This means that in a tree component, the minimum
possible number of isolated cities after the reform is 1 (zero is impossible).
For example, the root of the tree can be chosen as the isolated city.
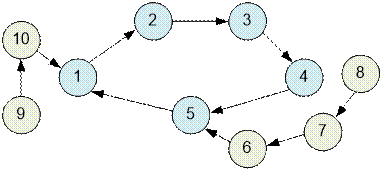
If a connected component contains a cycle,
its edges can always be oriented so that every vertex has at least one outgoing
edge.
The answer to the problem is the number of
connected components that do not contain cycles.
Example
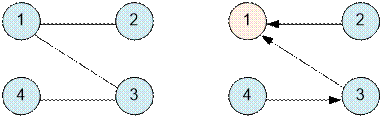
Consider the first example. The graph on
the left is the initial one, and the graph on the right is the graph after the
reform. Vertex 1 has no outgoing edges.
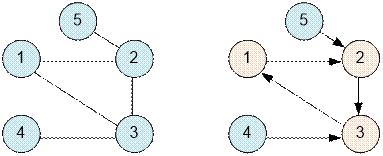
Let’s consider the second example. On the
left is the original graph, and on the right is the graph after the reform.
Each vertex has exactly one outgoing edge.
Algorithm implementation
Declare an adjacency list g to store the structure
of the graph, as well as an array used to mark already visited vertices.
vector<vector<int> > g;
vector<int> used;
The function dfs performs a depth-first
search starting from vertex v. The parent of vertex v is vertex p.
void dfs(int v, int p = -1)
{
used[v] = 1;
for (int to :
g[v])
{
if (to ==
p) continue;
If a cycle is detected in the current connected component,
set flag = 0.
if (used[to] == 1) flag = 0;
else dfs(to, v);
}
}
The main part of the program. Read the input data.
scanf("%d %d", &n, &m);
g.resize(n + 1);
used.resize(n + 1);
Read m edges and construct the graph.
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}
Perform depth-first search on a disconnected graph. The
variable res stores the number of connected components that contain no
cycles.
res = 0;
for (i = 1; i <= n; i++)
{
if (used[i] == 0)
{
Before processing each component, set
flag = 1. If a cycle is detected during the traversal, then after the dfs call completes, the value of flag will become 0.
flag = 1;
dfs(i);
res += flag;
}
}
Print the answer.
printf("%d\n", res);