9044. Одинокий
остров
Имеется множество островов,
соединенных односторонними мостами: если мост соединяет острова a и b, то мост может быть
использован только для перехода от a к b,
Вы не можете вернуться назад по этому мосту. Когда Вы находитесь на острове a,
то выбираете (равномерно и случайным образом) один из островов, на который можно
напрямую попасть с a через
односторонний мост, и переходите на этот остров. Вы застряните на острове, если
нельзя двигаться дальше. Гарантируется, что после того, как Вы покинете
какой-либо остров, то на него уже не сможете вернуться.
Найдите остров, на котором
Вы застряните с наибольшей вероятностью. Два острова считаются одинаково
вероятными, если абсолютная разность вероятностей попадания на них
≤ 10-9.
Вход. Первая строка содержит три
целых числа: количество островов n (1 ≤ n ≤ 200000), количество односторонних мостов m (1 ≤ m ≤ 500000) и номер r (1 ≤ r ≤ n) острова на котором Вы
сначала находитесь. Каждая из следующих m строк содержит два целых
числа ui и vi (1 ≤ ui, vi ≤ n)
описывающих односторонний мост из ui в vi.
Выход. Выведите номер острова, на
котором Вы застряните с наибольшей вероятностью. Если существует несколько
таких островов, то выведите их в порядке возрастания индексов (значения,
разделенные пробелом в одной строке).
|
Пример входа |
Пример выхода |
|
5 7 1 1 2 1 3 1 4 1 5 2 4 2 5 3 4 |
4 |
РЕШЕНИЕ
топологическая
сортировка
Анализ алгоритма
Запустим алгоритм Кана построения
топологическойсортировки. Для каждой вершины v
вычислим количество входящих InDegree[v] и исходящих OutDegree[v] из нее
ребер.
Обозначим через prob[v] вероятность оказаться в
вершине v. Изначально prob[r] = 1 для стартовой вершины r, для остальных вершин prob[v] = 0.
Далее для каждой вершины v в порядке топологической сортировки перебираем ребра (v, to) и увеличиваем значение prob[to] на prob[v] / OutDegree[v].
Застрять можно в вершине v, для которой OutDegree[v] = 0. Находим максимальное
значение среди prob[v], для которых OutDegree[v] = 0.
Пример
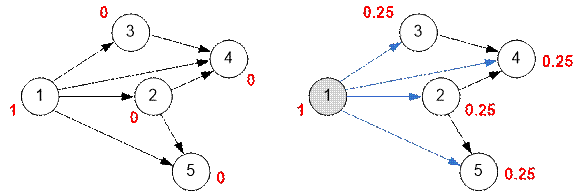
Промоделируем алгоритм Кана для
графа, заданного в условии. Возле вершин графа приписана вероятность попадания
в нее. Изначально (рисунок слева) вероятность нахождения во всех вершинах равна
0, кроме стартовой первой, вероятность пребывания в которой равна 1.
Первой вершиной топологического
порядка будет вершина 1. Из нее исходит 4 ребра, следовательно вероятность prob[1] = 1 будет разделена между 4 вершинами, а именно
значение prob[1] / 4 = 0.25 следует прибавить к prob[2], prob[3], prob[4] и prob[5].
Далее
вершина 2 будет занесена в топологический порядок. Из нее исходит два ребра. prob[2] / 2 = 0.125 следует
прибавить к prob[4] и prob[5] (левый рисунок снизу).
Следующей вершиной будет 3. Из нее исходит одно ребро. prob[3] / 1 = 0.25 прибавим к prob[4] (рисунок справа). Затем будут
обработаны вершины 4 и 5, однако они не содержат исходящих ребер и вероятности
пересчитываться не будут.
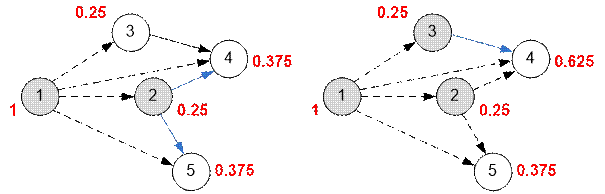
Тупиковая вершина (которая не
содержит исходящих ребер) с максимальной вероятностью попадания в нее имеет
номер 4. Такая вершина в графе одна.
Реализация
алгоритма
Объявим константу Epsilon.
#define EPS 1e-9
Граф храним в списке смежности graph. Объявим рабочие массивы.
vector<vector<int> > graph;
vector<int> InDegree, OutDegree;
deque<int> q;
vector<double> prob;
Читаем входные данные. Инициализируем массивы.
scanf("%d %d %d", &n, &m, &r);
graph.assign(n + 1, vector<int>());
InDegree.assign(n + 1, 0);
OutDegree.assign(n + 1, 0);
Читаем и строим граф. Для каждой
вершины подсчитываем количество входящих и исходящих ребер.
for (i = 0; i < m; i++)
{
scanf("%d %d", &a,
&b);
graph[a].push_back(b);
OutDegree[a]++;
InDegree[b]++;
}
Заносим в очередь вершины, в
которые не входят ребра.
for (i = 1; i < InDegree.size(); i++)
if (InDegree[i] == 0) q.push_back(i);
Вероятность оказаться в вершине r равна 1. Для остальных вершин начальная вероятность быть там равна
0.
prob.resize(n + 1);
prob[r] = 1;
Запускаем алгоритм Кана нахождения
топологической сортировки.
while (!q.empty())
{
Извлекаем из очереди вершину v. Перебираем
ребра (v, to). Из вершины v исходит OutDegree[v] ребер. Вероятность нахождения в вершине v равна prob[v]. Следовательно вероятность попадания из v в to равна prob[v] / OutDegree[v]. Эту
вероятность и следует прибавить к prob[to].
v = q.front(); q.pop_front();
for (i = 0; i < graph[v].size(); i++)
{
to = graph[v][i];
prob[to] += prob[v] / OutDegree[v];
Уменьшаем количество входящих
ребер в вершину v.
InDegree[to]--;
Если в вершину to не входит ни
одно ребро, то заносим to в очередь.
if (InDegree[to] == 0) q.push_back(to);
}
}
Ищем максимальное значение
вероятности среди prob[v] при условии что из острова v нет выхода.
mx = 0;
for (i = 1; i <= n; i++)
if (OutDegree[i] == 0 && prob[i] > mx) mx = max(mx, prob[i]);
Выводим вершины (их может быть
несколько), на которых достигается максимальная вероятность.
for (i = 1; i <= n; i++)
if (OutDegree[i] == 0 && fabs(prob[i] - mx) <= EPS)
printf("%d ", i);