9061. Светский
прием
Агент Джонни Инглиш снова в деле!
На этот раз бесстрашному агенту и
его помощнику Бофу поручено проследить за порядком на благотворительном
мероприятии. Войдя в зал и осмотревшись, Инглиш понял, что для полной картины
происходящего ему придётся немного прогуляться по залу, перекинуться парой слов
с гостями и понаблюдать за официантами. Закончив разведку, Инглиш, уверенный в
успехе, решил встретиться с Бофом и блеснуть перед ним своими невероятными
аналитическими способностями. К сожалению, бедняга Боф на светских мероприятиях
совершенно теряется, поэтому просто медленно следует за указаниями старшего агента.
Зал представляет собой квадрат на
координатной плоскости со сторонами длиной 106, параллельными
координатным осям. Вход находится в левом нижнем углу квадрата, в точке O(0, 0).
Агент Инглиш собирается выбрать несколько гостей, расположенных в точках с
целыми координатами, и поздороваться с каждым по очереди. Он не будет
здороваться с одним и тем же гостем подряд, но иногда может ошибиться и
вернуться к гостю, с которым уже здоровался. Тренированный агент движется со
скоростью p, а здоровается с гостями мгновенно. В это время Боф,
двигаясь со скоростью q, направляется напрямую к финальной точке
маршрута, намеченного Инглишем.
Чтобы не вызывать подозрений,
агент Инглиш хочет найти такой маршрут, при котором они с Бофом прибудут в
точку встречи одновременно. К сожалению, у агента нет времени продумывать
детали своего гениального плана, поэтому этим предстоит заняться Вам.
По заданным скоростям q и p
найдите любой маршрут, начинающийся в точке (0, 0) и состоящий из точек с
неотрицательными координатами, не превосходящими 106. При этом время
прохождения маршрута со скоростью q должно совпадать с временем
прохождения того же маршрута со скоростью p.
Вход. В одной строке заданы два
натуральных числа q и p (1 ≤ q ≤ p ≤ 105)
– скорости Бофа и агента Инглиша соответственно.
Выход. В первой строке выведите число n
(2 ≤ n ≤ 100) – количество точек в маршруте. В следующих n
строках выведите пары целых чисел x и y (0 ≤ x, y
≤ 106) – координаты точек в порядке обхода. Первой обязательно
должна быть выведена точка (0, 0). Точки могут повторяться, однако в маршруте
не должно быть двух одинаковых точек подряд.
|
Пример
входа 1 |
Пример
выхода 1 |
|
1 2 |
4 0 0 2 0 2 1 2 0 |
|
|
|
|
Пример
входа 2 |
Пример
выхода 2 |
|
1 3 |
4 0 0 2 0 2 2 2 0 |
РЕШЕНИЕ
конструктив
Анализ алгоритма
Джонни Инглиш и Боф достигают
конечной точки одновременно за время t. Джонни Инглиш преодолевает расстояние
s1 = p * t, а Боф s2 = q
* t. Отношение пройденных расстояний равно отношению скоростей: s1
/ s2 = p / q.
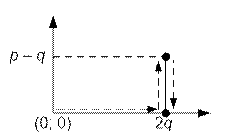
Построим такие пути конструктивно. Рассмотрим, например, маршрут из 4 точек: (0, 0) → (2q, 0) → (2q, p – q) → (2q, 0).
Здесь выбрана
координата p – q, чтобы ее значение было неотрицательным (по
условию задачи q ≤ p).
·
Длина пути Джонни Инглиша равна 2q +
2 * (p – q) = 2p.
·
Длина пути Бофа равна 2q.
Если скорости Джонни Инглиша и Бофа
одинаковы, то точки (2q, 0) и (2q, p – q) совпадают,
а по условию задачи на маршруте не может быть двух одинаковых точек подряд. В
этом случае в качестве решения можно выбрать, например, следующий маршрут: (0,
0) → (1, 0).
Реализация алгоритма
Читаем
входные данные.
scanf("%d %d", &q, &p);
Если
скорости Джонни Инглиша и Бофа одинаковы, то они движутся из точки (0, 0) в
точку (1, 1).
if (q == p)
{
printf("2\n");
printf("%d %d\n", 0, 0);
printf("%d %d\n", 1, 0);
return 0;
}
Если p
≠ q, то маршрут состоит из четырёх точек.
printf("4\n");
printf("%d %d\n", 0, 0);
printf("%d %d\n", 2 * q, 0);
printf("%d %d\n", 2 * q, p - q);
printf("%d %d\n", 2 * q, 0);