9063. Greek car

After long journeys and wanderings, in one temple Kratos discovered an interesting find – a Greek car. It was one of the first prototypes that worked on clean energy. In the same temple, Kratos also found fuel – a fountain containing a litres of clean energy.

Kratos knows that 1 litre of clean energy is enough to cover 100 kilometers. However, there is one problem - the tank of the machine is designed so that no more than 1 litres of energy can be placed in it, and energy can only be replenished in the temple. However, having carefully studied the structure of this clean energy, Kratos realized that he could pour off it to the ground and leave it on the ground, and then return and put it into the tank without loss. Now he is interested in the question – what is the maximum distance he can travel on the machine he found?

Input. One real number а (0.0 ≤ a ≤ 2.0) – the number of litres of clean energy in the fountain.

Output. Print the maximum distance that Kratos can travel on the machine found. The answer should be displayed with an accuracy of 6 decimal places.

Sample input	Sample output
1.000000	100

SOLUTION

mathematics

Algorithm analysis

Using 1 liter of clean energy, Kratos can travel 100 kilometers. If a ≤ 1.0 liter of energy available, then maximum can be overcome 100 kilometers by pouring initially all the energy into the tank.

Consider the case 1.0 < a ≤ 2.0. Let the tank be initially filled with 1 liter of energy. The car goes forward, spending x liters, left (1 – 2x) liters on the ground and come back, spending the last x liters taken with it.

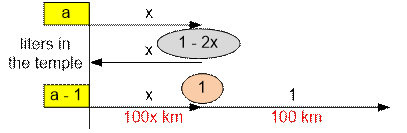
There are a – 1 liters of energy left in the temple, Kratos is pouring them into the tank. Having reached the place where the unused energy remains, and having used x liters, he must take all of it, filling the tank to 1. In this case, he will get as far as possible, spending all the available energy. When Kratos reaches the energy left on the ground, he will have (a – 1 – x) liters of fuel in the tank. After adding the energy left on the ground (1 – 2x), the tank should be filled to the end. The next condition must be satisfied: (a – 1 – x) + (1 – 2x) = 1. Solve the equation: a – 3x = 1, or x = (a – 1) / 3. Kratos’ car will travel maximum

100x + 100 = 100 * (a – 1) / 3 + 100

kilometers.

Algorithm realization

Read the input data.

scanf("%lf", &a);

Compute the result res depending on the value of a.

if (a <= 1)

res = 100 * a;

else

res = 100 + 100 * (a - 1) / 3;

Print the answer.

printf("%.6lf\n", res);